Figure 1. A ring of radius R and charge +Q lies in the x,y-plane. Point P is distance a from the centre of the ring.

Sunday, 26 August 2018

1:17 AM

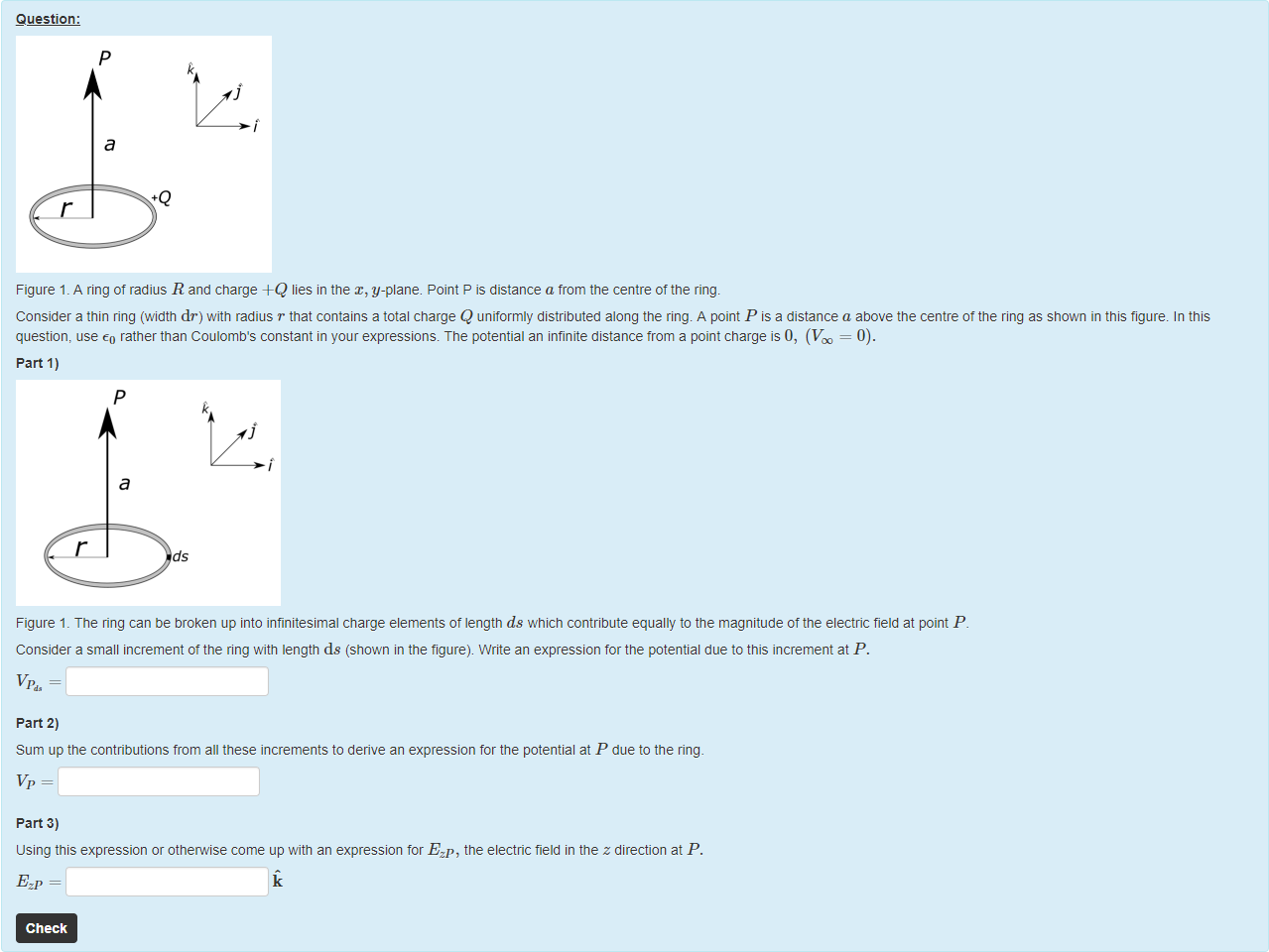
Machine generated alternative text: Question: p a Figure 1 _ A ring of radius R and charge A-Q lies in the x, y-plane. Point P is distance a from the centre of the ring. Consider a thin ring (width dr) with radius T that contains a total charge Q uniformly distributed along the ring. A point P is a distance a above the centre ot the ring as shown in this figure. In this question, use eo rather than Coulomb's constant in your expressions. The potential an infinite distance trom a point charge is 0, (Vm = 0). part 1) a ds Figure 1 _ The ring can be broken up into infinitesimal charge elements ot length ds which contribute equally to the magnitude of the electric field at point P. Consider a small increment ot the ring with length ds (shown in the figure). Write an expression for the potential due to this increment at P. part 2) Sum up the contributions from all these increments to derive an expression for the potential at P due to the ring. part 3) using this expression or otnemise come up with an expression for Ezp, the electric field in the z direction at P. Ezp Check

 

Machine generated alternative text: Feedback tor Part 1) Solve this using the equation tor the potential due to a point charge. 4TE0 r In this case, q = QG , as is the length of the increment divided by the circumference, this tells you the proportion ot Q on the increment The distance ot the increment from P is d = r2 -Fa2, so: Q ds v P ds 4TEo 2 Tr V/r2 a2 Marks for this submissiom 0.00/0.33. This submission attracted a penalty of 0.11 Feedback tor Part 2) We need to sum the increments all around the circle. Relating angle to s we have so ds r dB. We can write: VPds = 27r. So: Qrd9 47rEo 2Trrv/r2+a2 Then to add all the increments around the ring we integrate from 9 = Oto 9 Marks for this submissiom 0.00/0.33. This submission attracted a penalty of 0.11 1 102m Qr dB 47rE0 JO 27rr v/r2+a2 Qr 4 • 27T a2 47rE0 x 2m 4 V/r2 a2

 

Machine generated alternative text: Feedback tor Part 3) The electric field in the z direction is given by: In order to perform this differentiation we need to know now V changes as z changes, in this case a tells us the distance along the z axis from the centre of the ring, near P we can write Q 47rE0 r2 _4_z2 47rE0 dz r2+z2 At P, z 47rE0 = a so: Q + z2) 1/2) 47rE0 dz • (—1/2) • (2z) • (r2 + z2)3/2 Q 47rE0 (r2+z2)3/2 • Q. 47rE0 (r24_a2 ) 3/2 Marks for this submissiom 0.00/0.33. This submission attracted a penalty of 0.11 A correct answer is , which can be typed in as follows: A correct answer is , which can be typed in as follows: A correct answer is which can be typed in as follows:

 

 

Created with Microsoft OneNote 2016.