Figure 1. A charged rod of length l and linear charge density λ sits vertically in the y-direction. Point P sits a distance a from the base of the rod.
Sunday, 26 August 2018
1:10 AM
|
|
|||
|
|
 ![Untitled picture.png Machine generated alternative text:
part 3)
using this expression or otnemise come up with an expression for Exp, the electric field in the x direction at P.
Untitled picture.png Machine generated alternative text:
Feedback tor Part 1)
The charge on the increment q = dy, the distance of the increment trom P is given by d
a2 + Y2. We can substitute these into the expression for a potential due to a point charge.
47rE0 r
dy
v Pdy = k v/y2+a2
Marks for this submissiom 0.00/0.33. This submission attracted a penalty of 0.11
Feedback tor Part 2)
We sum each ottne increments by integrating between y = 0 and y = l.
v — Ilk
dy
v/y24-a2
dy.
0 •v/y24-a2
This is a standard integral so:
= [In(l+ 12
- A [In(l+ 12+a2) -In(a)]
= kA1n(
Marks for this submissiom 0.00/0.33. This submission attracted a penalty of 0.11
Untitled picture.png Machine generated alternative text:
Feedback tor Part 3)
The electric field in the direction is given by:
In order to perform this differentiation we need to know now V changes as changes, in this case distance along the axis is given by a, so near P we can write
Vp = 12 + — In(x))
along the axis perpendicular to the bottom of the rod where x is the distance trom the bottom of the rod. So:
(In(l + 12 + x2) — In(x))
1
12+x2x(1+ 12+x2)
12+x2(1+ 12+x2)
12+x2(1+ 12+x2)
12+x2)
12+x2(1+ 12+x2)
At P,
= a so:
12+a2
Marks for this submissiom 0.00/0.33. This submission attracted a penalty of 0.11
A correct answer is
, which can be typed in as follows:
/ sqrt(yA2+aA2)
A correct answer is k • In 12 + a2 + I — In(a)) • A, which can be typed in as follows:
A2+aA2 )
A correct answer
, which can be typed in as follows:
a, 4.a2
/ (a'sqrt(1A2+aA2) )
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings







](Figure%201.%20A%20charged%20rod%20of%20length%20l%20and%20linear%20charge%20density%20λ%20sits%20vertically%20in%20the%20y-direction.%20Point%20P%20sits%20a%20distance%20a%20from%20the%20base%20of%20the%20rod._files/image002.png)  |
||
|
|
 |
||
|
|
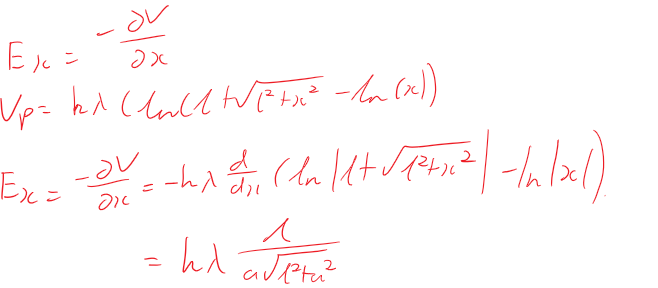Figure 1. A charged rod of length l and linear charge density λ sits vertically in the y-direction. Point P sits a distance a from the base of the rod.
Sunday, 26 August 2018
1:10 AM
|
|
|||
|
|
|
||
|
|
|
||
|
|
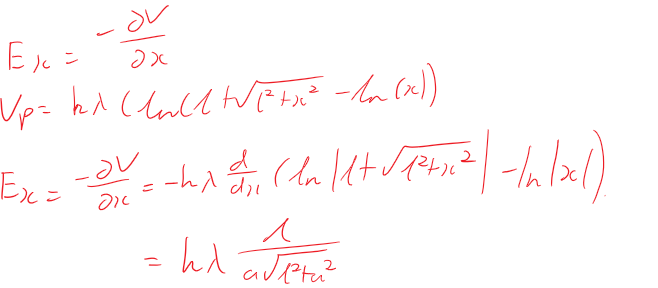Created with Microsoft OneNote 2016.