“How much information can be (successfully) transmitted in the presence of noise?”

Let $A$ be the source (input), and $B$ be the sink (output).

In general, we want to figure out $P(b_i | a_i)$, for all possible $i$’s

Baye's Rule

$P (a_j and b_i ) = P (a | j ) P(b_i | a_j ) = P (b_i ) P(a_j | b_i )$

$P(a_j | b_i) = {P(a_j) P (b_i | a_j)}/{\Sum_j P(a_j) P(b_i|a_j)}

Entropy

Input entropy: $H(A) = -\Sum P(a_j) log P(a_j)#
Output entropy: $H(A) = -\Sum P(b_i) log P(b_i)#

Conditional Entropy

B given $a_j$ = $H(B | a_j) = -\Sum P(b_i|a_j) log P(b_i|a_j)$
A given $b_i$ = $H(A | b_i) = -\Sum P(a_j|b_i) log P(a_j|b_i)$

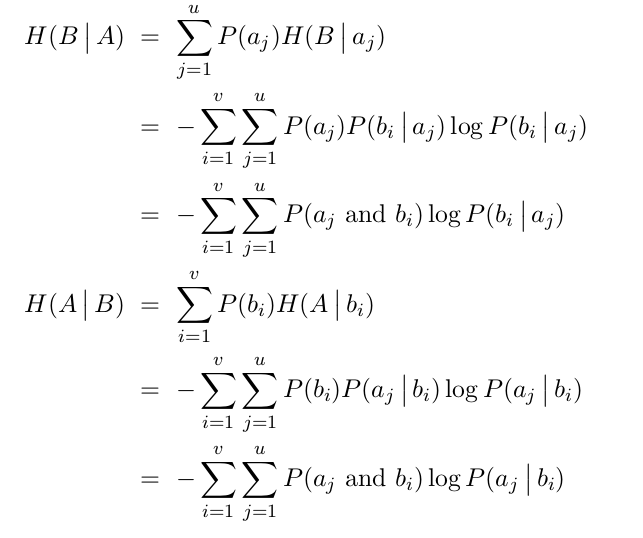
The equivocation of a channel is H(A|B)

Joint Entropy

H(A and B) = H(A,B) = H(B,A) is $-\Sum \Sum P(a_j and b_i) log P(a_j and b_i)

== H(A) + H(B|A) == H(B) + H(A|B)

Binary Symmetric Channel (BSC)

• $p$ - Crossover probability
• $x$ - Probability of sending a given symbol (ie 0)

$H(x) = −x log(x) − (1−x) log(1−x)$