Midsem
Monday, 8 July 2019
3:01 PM

|
|
|||||||
|
|
|
||||||
|
|
![Machine generated alternative text:
ans
sum (poisspdf ( [O: 6] , 7 . 6) )
0.6354](Midsem_files/image003.png) |
||||||
|
|
|||||||
|
|
 |
||||||
|
|
|||||||
|
|
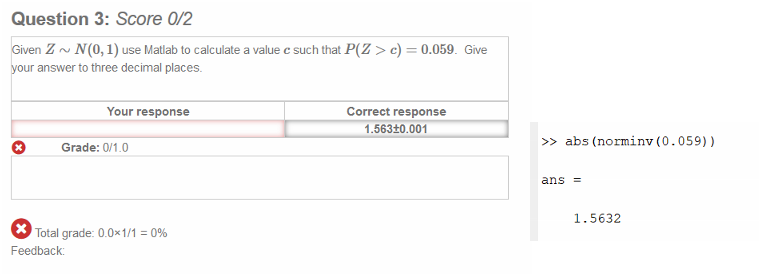 |
||||||
|
|
|||||||
|
|
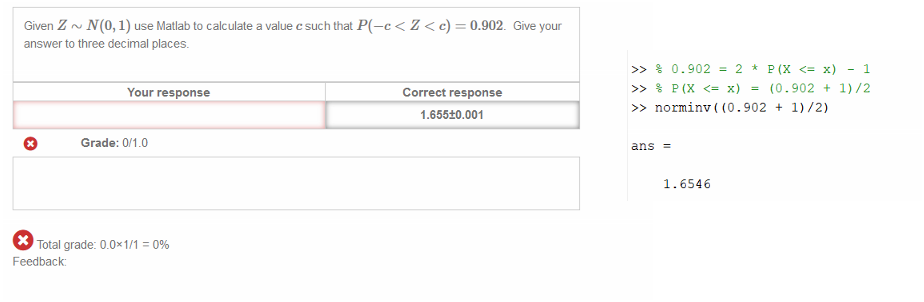 |
||||||
|
|
|||||||
|
|
|||||
|
|
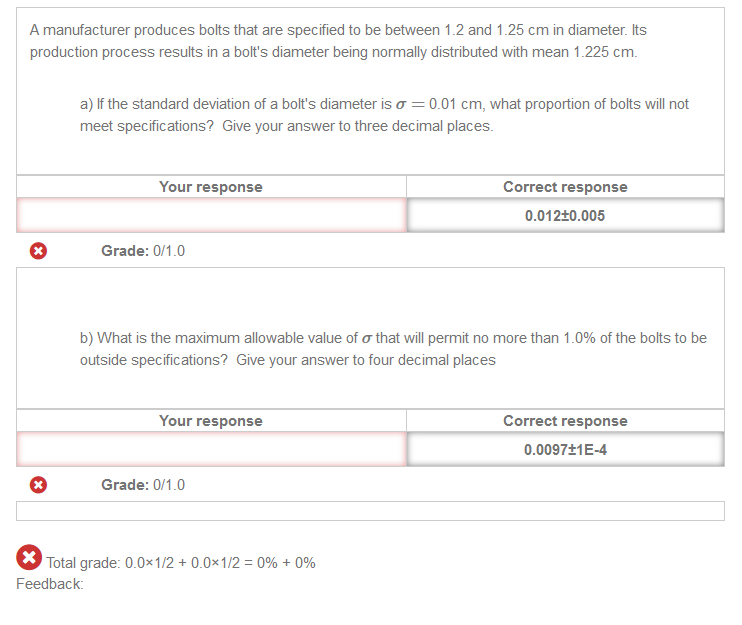 |
 |
|||
|
|
|||||
|
|
|
||||
|
|
|||||
|
|
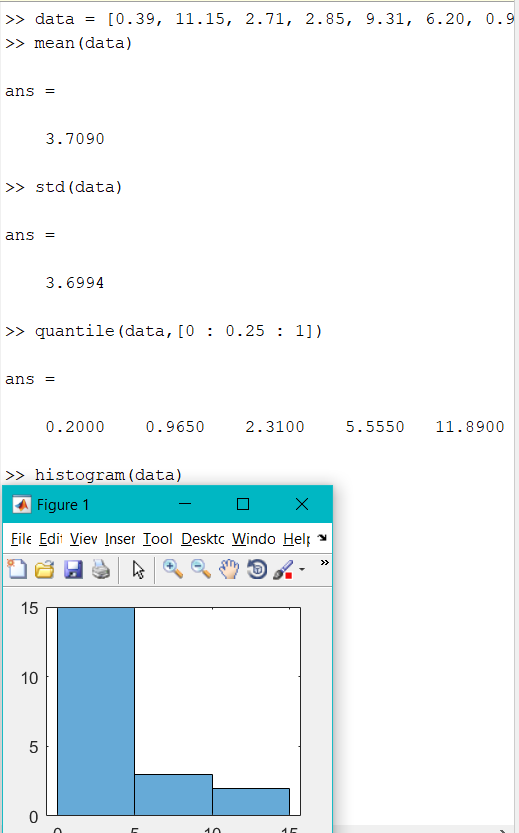 |
||||
|
|
|||||
|
|
||||
|
|
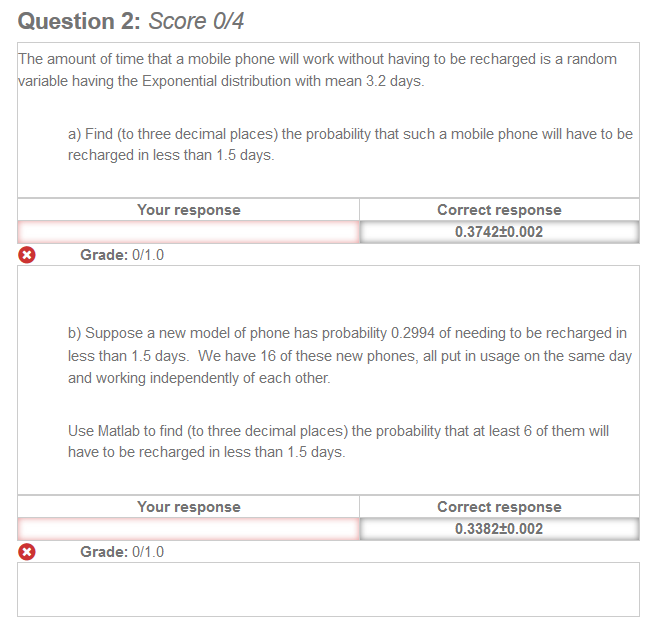 |
|||
|
|
 |
|||
|
|
||||
|
|
 |
|||
|
|
||||
|
|
||||||||
|
|
![Untitled picture.png Machine generated alternative text:
Question 4: Score 0/4
Diameters of the trees in a forest are normally distributed with mean = 380 cm and standard
eviatlon a = 6.0 cm. The trees that can be used as timber must have specific Size. The
lameters must lie in the interval [24.8, 51 2] cm in order to be used as timber.
) In the forest, what fraction of trees cannot be used as timber? Give your answer to three
ecimal places.
Correct response
0.028±0.005
O
Your response
Grade: 0/1.0
b) To what value must the standard deviationa be reduced is required that 984% of the
rees can be used as timber? Give your answer to two decimal places.
O
Your response
Grade: 0/1.0
Correct response
5.48±0.01
Total grade: o_0X1/2 + o_0X1/2 = +
Feedback:
Untitled picture.png Machine generated alternative text:
>> (51.2-38)/6
ans
-2.2))
ans
2.2000
(normcdf (2 . 2)
0.0278
normcdf (
Untitled picture.png Machine generated alternative text:
ans
ans
98.4/100/2
0.4920
0.0080
.5
98 .4/100/2
>> norminv(.5
ans
-2.4089
51.2
ans
13.2000
(51.2
ans
5.4797
38
38)
98 .4/100/2)
2.4089
Screen clipping taken: 10/07/2019 2:01 PM](Midsem_files/image017.png)    |
|||||||
|
|
 |
|||||||
|
|
||||||||
|
|
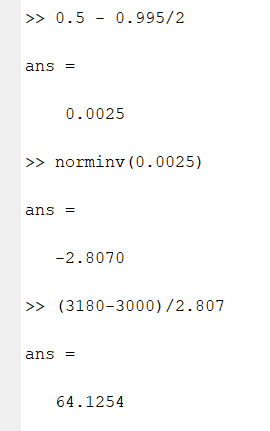 |
|||||||
|
|
||||||||
|
|
 |
|||||||
|
|
||||||||
|
|
 |
|||||||
|
|
||||||||
|
|
 |
|||||||
|
|
||||||||
Midsem
Monday, 8 July 2019
3:01 PM

|
|
|||||||
|
|
|
||||||
|
|
![Machine generated alternative text:
ans
sum (poisspdf ( [O: 6] , 7 . 6) )
0.6354](Midsem_files/image003.png) |
||||||
|
|
|||||||
|
|
 |
||||||
|
|
|||||||
|
|
 |
||||||
|
|
|||||||
|
|
 |
||||||
|
|
|||||||
|
|
|||||
|
|
 |
 |
|||
|
|
|||||
|
|
|
||||
|
|
|||||
|
|
 |
||||
|
|
|||||
|
|
||||
|
|
 |
|||
|
|
 |
|||
|
|
||||
|
|
 |
|||
|
|
||||
|
|
||||||||
|
|
![Untitled picture.png Machine generated alternative text:
Question 4: Score 0/4
Diameters of the trees in a forest are normally distributed with mean = 380 cm and standard
eviatlon a = 6.0 cm. The trees that can be used as timber must have specific Size. The
lameters must lie in the interval [24.8, 51 2] cm in order to be used as timber.
) In the forest, what fraction of trees cannot be used as timber? Give your answer to three
ecimal places.
Correct response
0.028±0.005
O
Your response
Grade: 0/1.0
b) To what value must the standard deviationa be reduced is required that 984% of the
rees can be used as timber? Give your answer to two decimal places.
O
Your response
Grade: 0/1.0
Correct response
5.48±0.01
Total grade: o_0X1/2 + o_0X1/2 = +
Feedback:
Untitled picture.png Machine generated alternative text:
>> (51.2-38)/6
ans
-2.2))
ans
2.2000
(normcdf (2 . 2)
0.0278
normcdf (
Untitled picture.png Machine generated alternative text:
ans
ans
98.4/100/2
0.4920
0.0080
.5
98 .4/100/2
>> norminv(.5
ans
-2.4089
51.2
ans
13.2000
(51.2
ans
5.4797
38
38)
98 .4/100/2)
2.4089
Screen clipping taken: 10/07/2019 2:01 PM](Midsem_files/image017.png)    |
|||||||
|
|
 |
|||||||
|
|
||||||||
|
|
 |
|||||||
|
|
||||||||
|
|
 |
|||||||
|
|
||||||||
|
|
 |
|||||||
|
|
||||||||
|
|
 |
|||||||
|
|
||||||||
Created with Microsoft OneNote 2016.