Covariance of Two Random Variables

Tuesday, 2 July 2019

3:02 PM

The covariance is defined by

 

 

---

 

 

 

  • The unit of  is the unit of  multiplied by the unit of

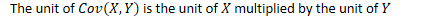
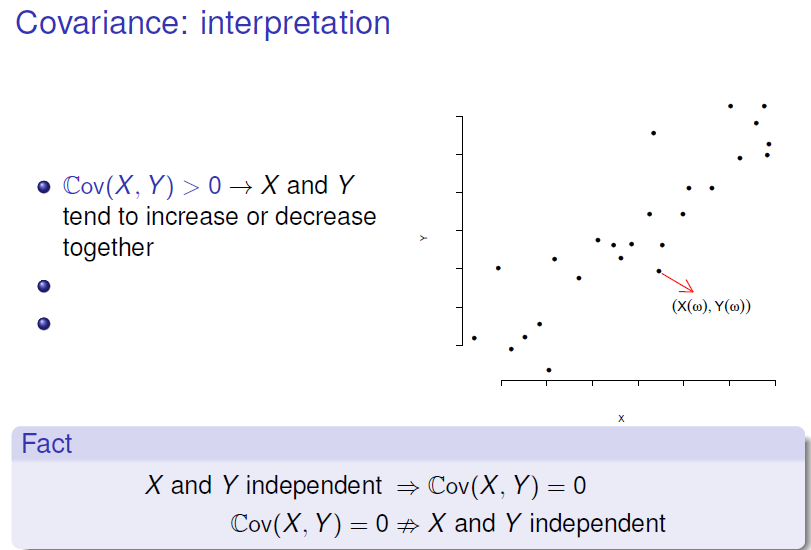
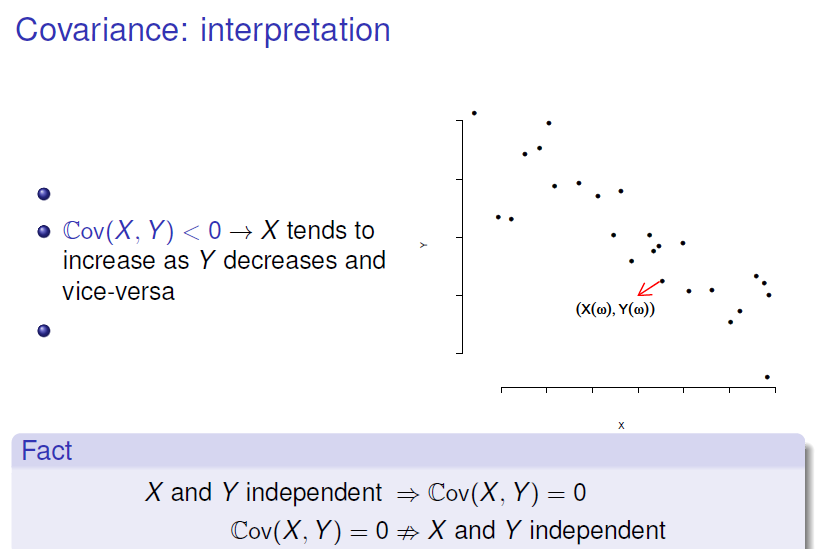
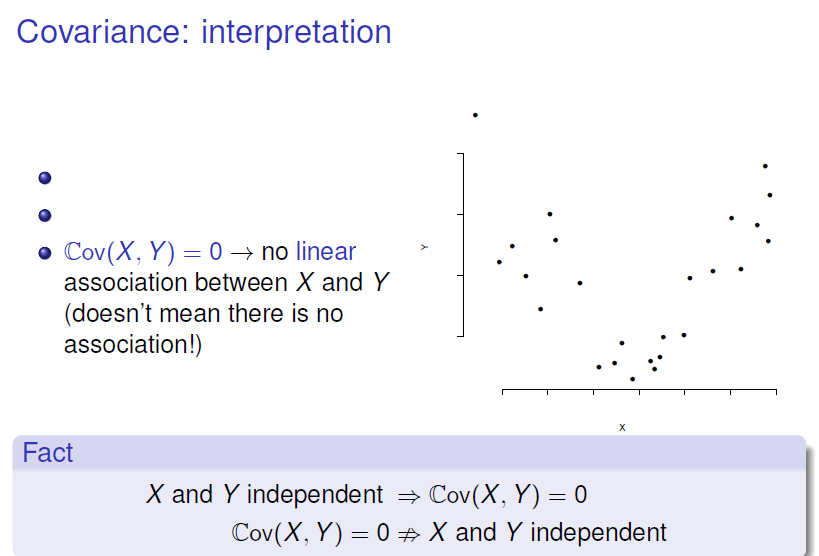
Covariance: interpretation Suppose X and Y are two Bernoulli random variables. Then, XY is also a Bernoulli random variable which takes the value I if and only if X I and Y I. It follows: cov(X, Y) l, Y 1) Then, cov(X, Y) > O = 1, Y = 1) > = = 1) IIX - 1) > - 1) * The outcome X = 1 makes it more likely that Y = 1 —+ Y tends to increase when X does, and vice-versa This result holds for any r.v. X and Y (not only Bernoulli r.v.).

 

Covariance: interpretation cov(x, Y) > X and Y tend to increase or decrease together Fact X and Y independent Cov(X, Y) = O Cov(X, Y) = 0 X and Y independent

 

Covariance: interpretation Cov(X, Y) < O X tends to increase as Y decreases and vice-versa (XO, YO) Fact X and Y independent Cov(X, Y) = O Cov(X, Y) 0 X and Y independent

 

Covariance: interpretation Cov(X, Y) = 0 no linear association between X and Y (doesn't mean there is no association!) Fact X and Y independent Cov(X, Y) = O Cov(X, Y) O X and Y independent

 

 

Created with Microsoft OneNote 2016.