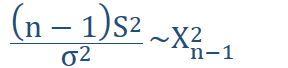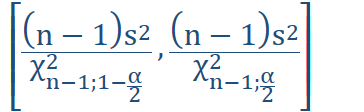Chi-square Distribution

Sunday, 18 August 2019

8:12 PM

Sampling distribution of  when the population is normal

 

 

If  is a random sample from a normal population with mean  and variance  then

 

Where  denotes the chi-square distribution with  degrees of freedom

 

 

Machine generated alternative text: 8. Inferences concerning a varianæ The x2-distribution 8.2 Estimation ot a variance A random variable, say X, is said to follow the chi-square-distribution with v degrees of freedom, i.e. if its probability density function is given by 1 17/2-1 -x/2 f(x) — for x > 0 x = [0, +00) 2v/2r (U) for some integer v Note: the Gamma function is given by xy 1 e-x dx It can be shown that r (y) (y 1) x r (y — 1), so that, if y is a positive for y > 0 integer n, There is usually no simple expression for the x2-cdf. MATH20gg,'285g (Statistics) Dr Jia Deng

 

NOT SYMMETRIC

 

Confidence interval:

 

 

 

 

 

Created with Microsoft OneNote 2016.