Calc1231W7T1 - Population growth
Wednesday, 5 September 2018
12:14 PM
|
|
|||||
|
|
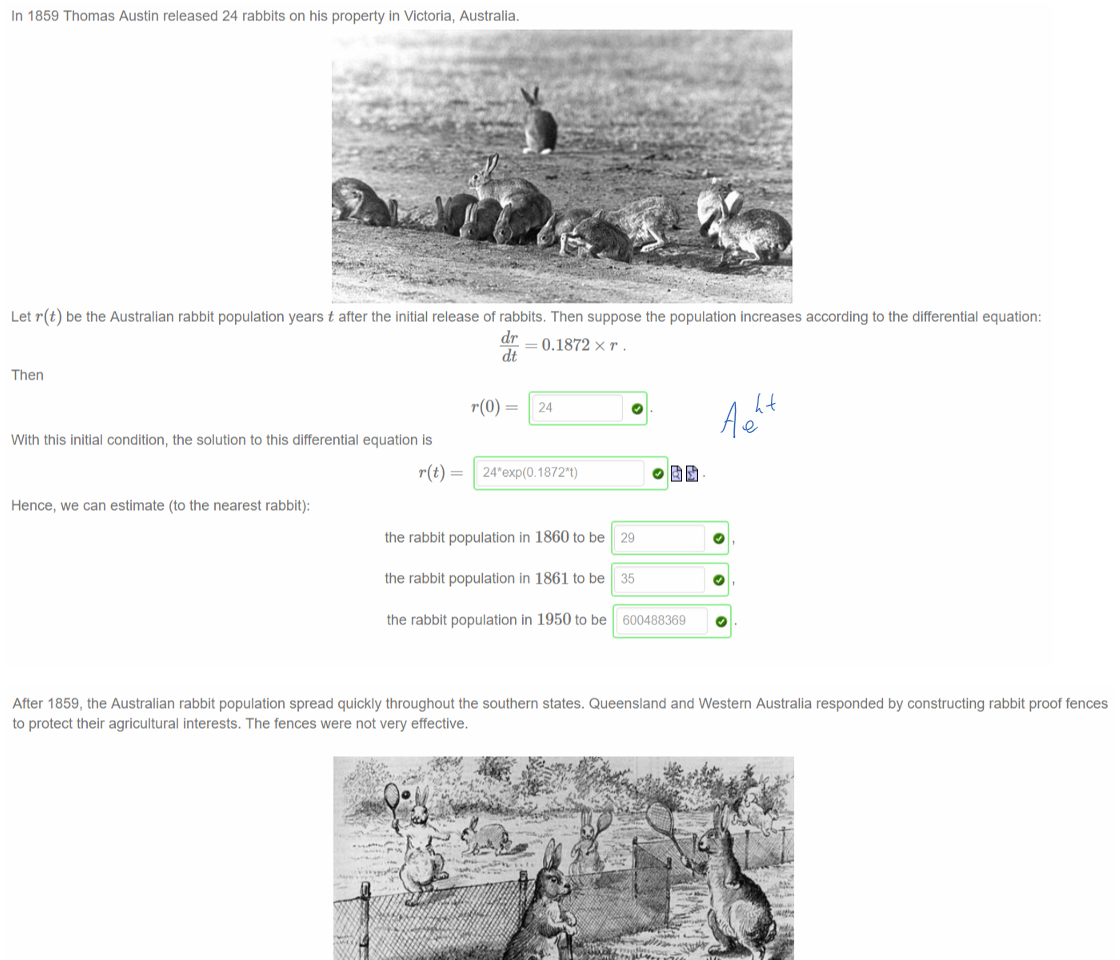     |
||||
|
|
|
||||
|
|
|||||
|
|
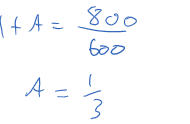 |
||||
|
|
|||||
Calc1231W7T1 - Population growth
Wednesday, 5 September 2018
12:14 PM
|
|
|||||
|
|
     |
||||
|
|
|
||||
|
|
|||||
|
|
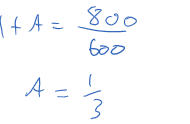 |
||||
|
|
|||||
Created with Microsoft OneNote 2016.