Calc1231W5T3 - Integration by circle trig substitution
Friday, 24 August 2018
1:05 PM





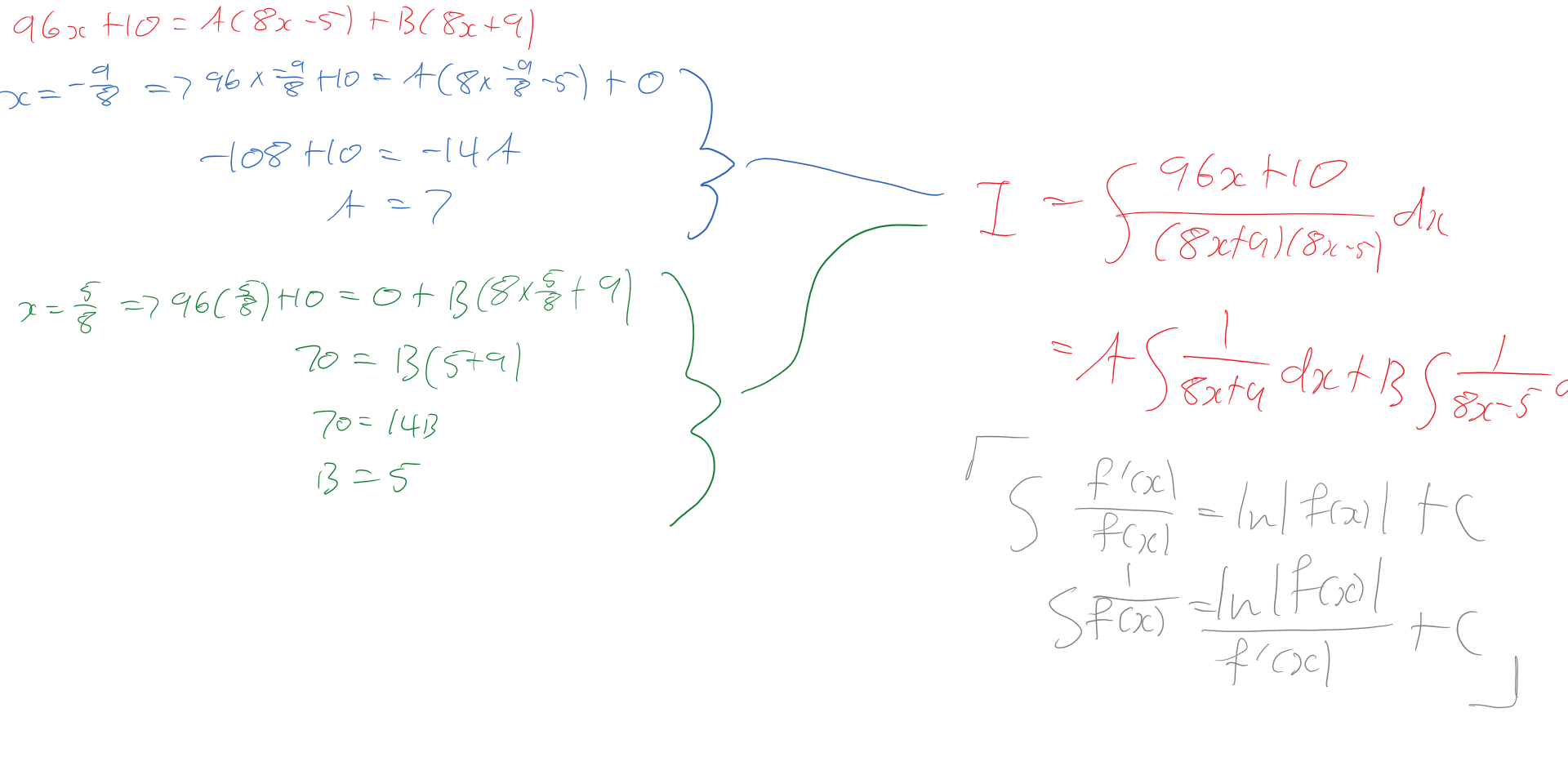
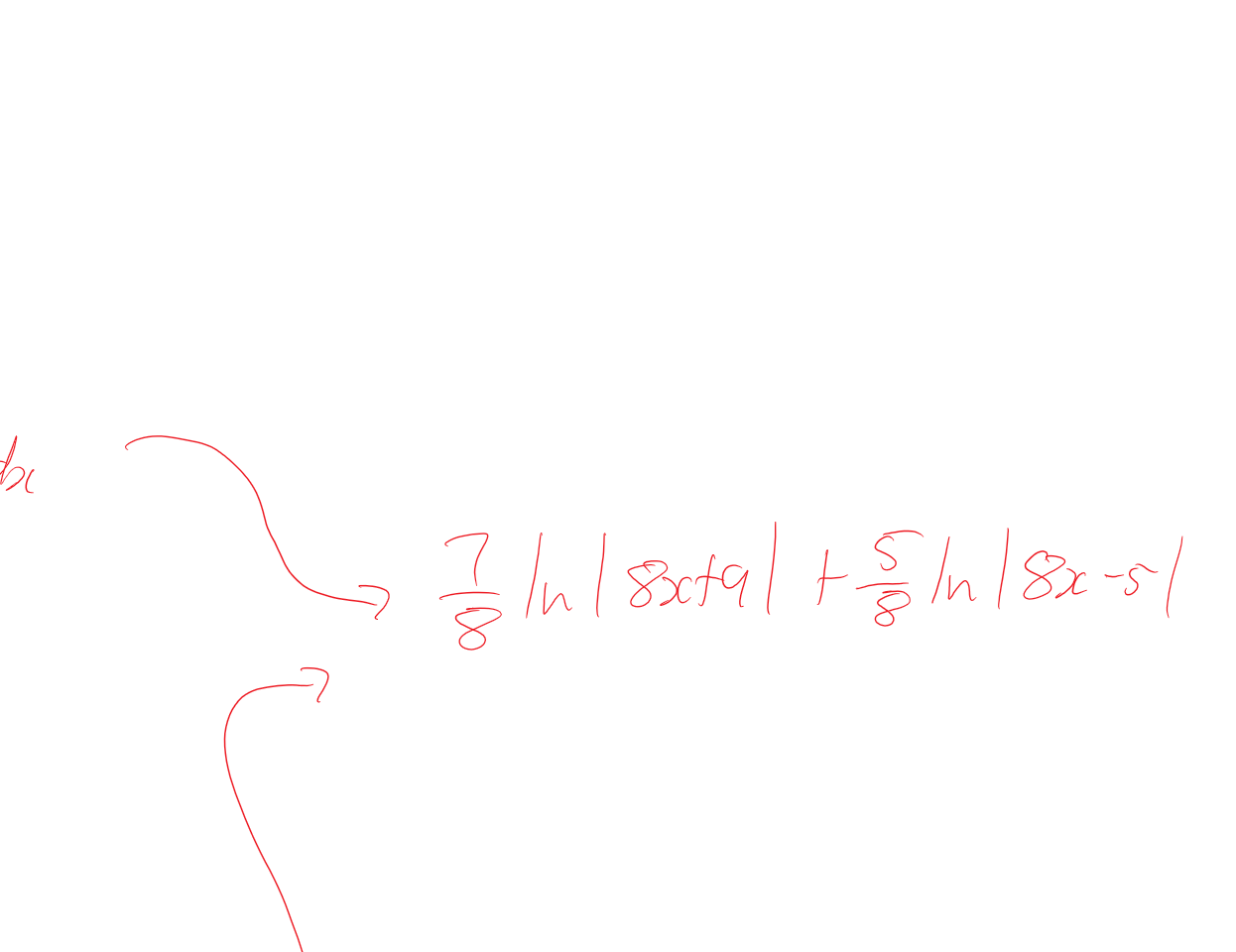


|
|
|||
|
|
 |
||
|
|
|
||
|
|
|
|
|||||||||||||
|
|
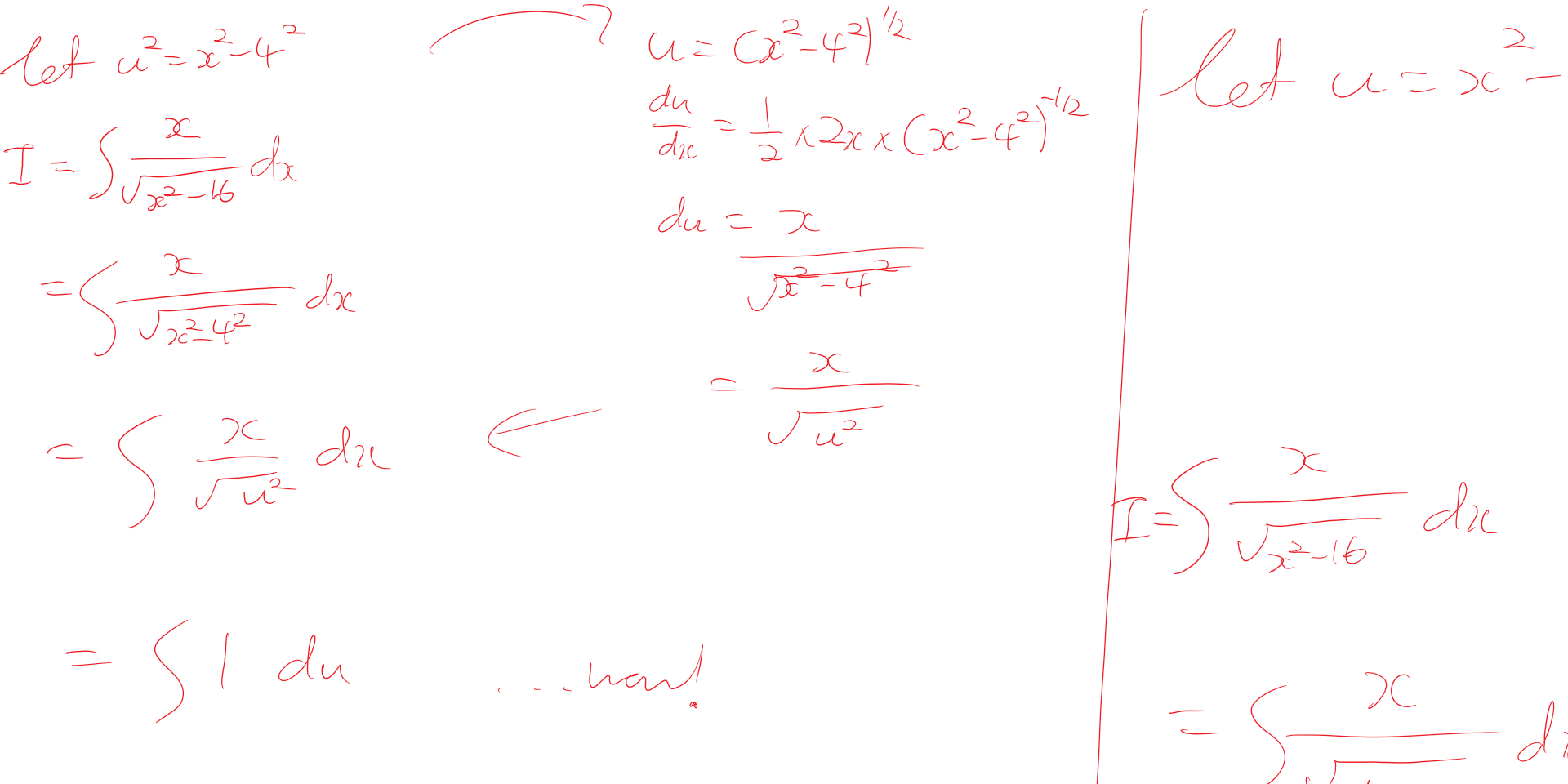 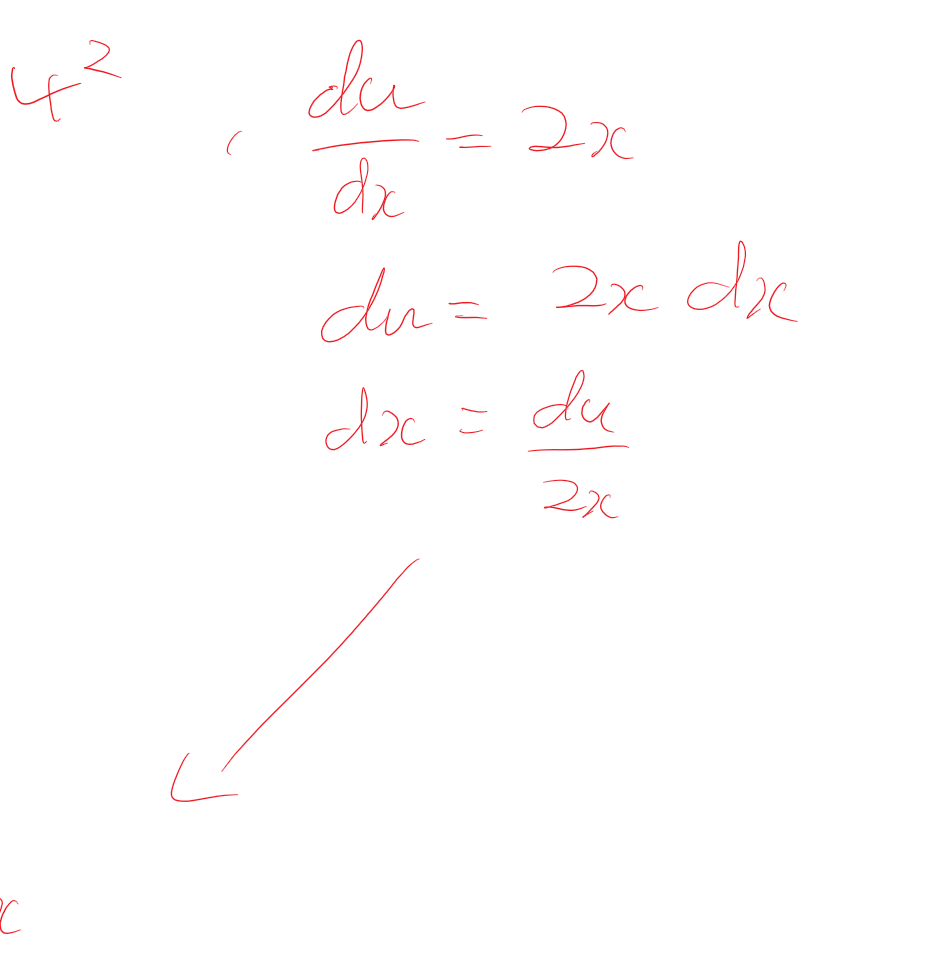 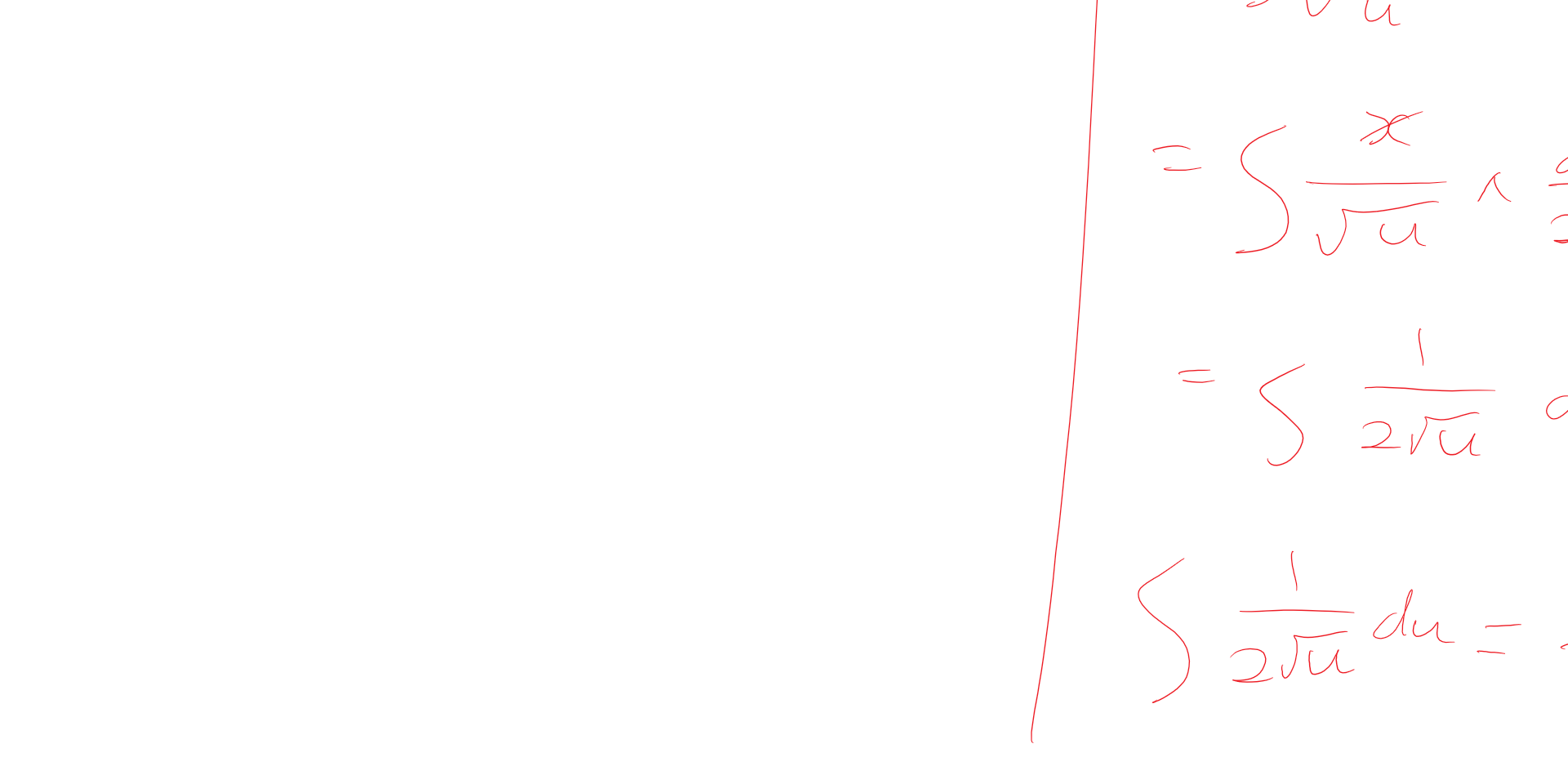 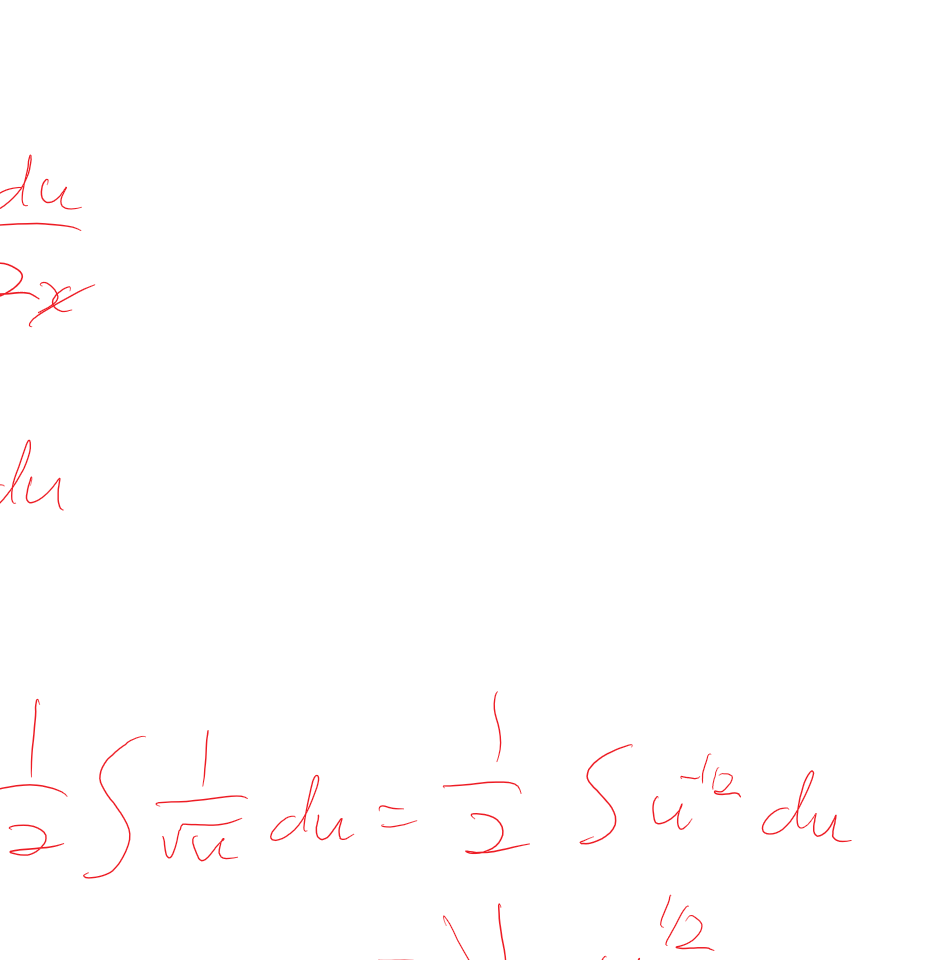  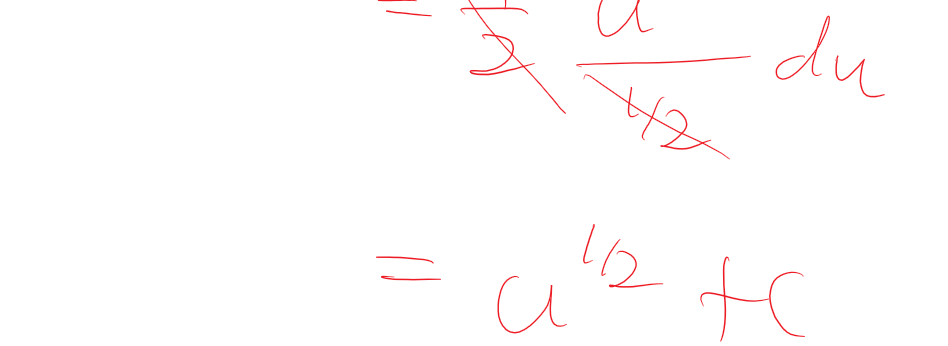 |
||||||||||||
|
|
|||||||||||||
|
|
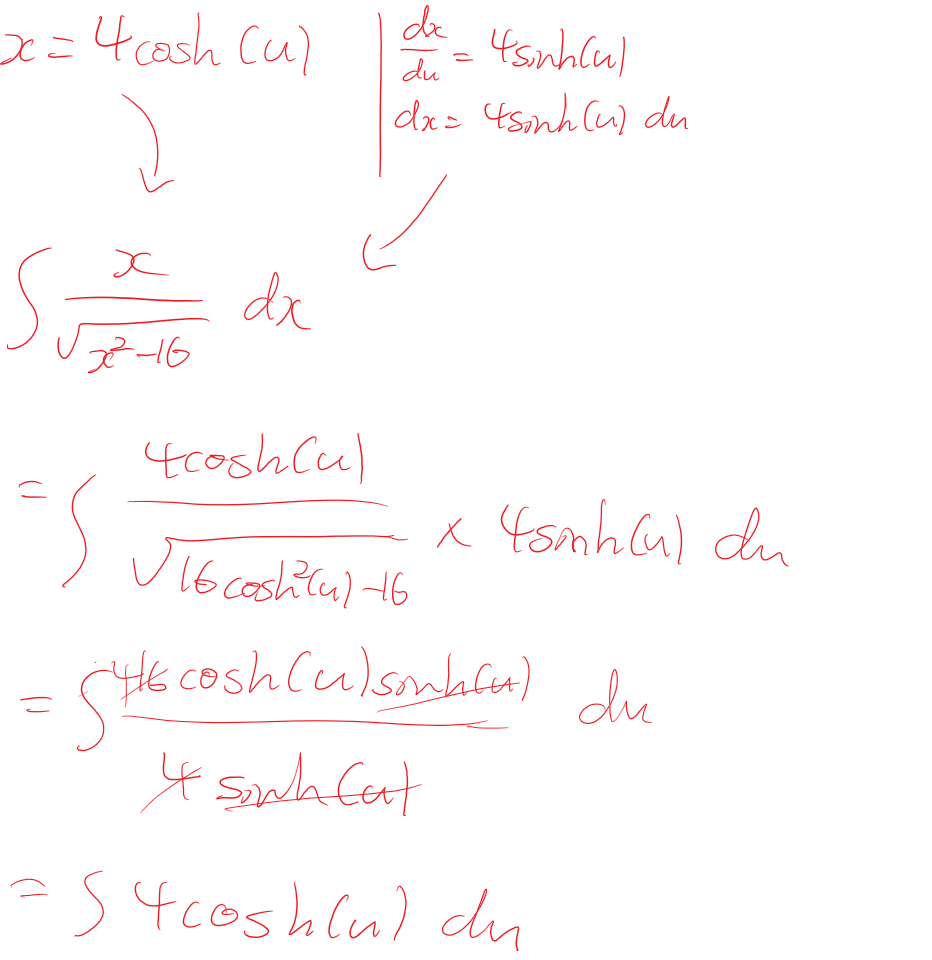 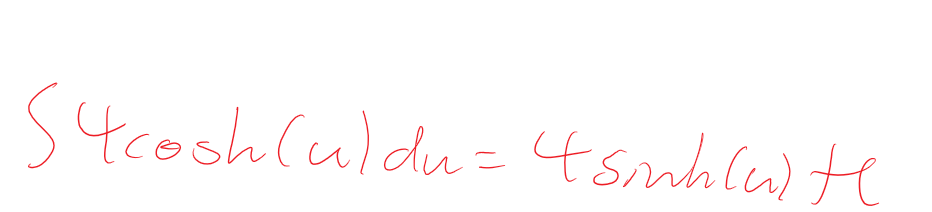 |
||||||||||||
|
|
 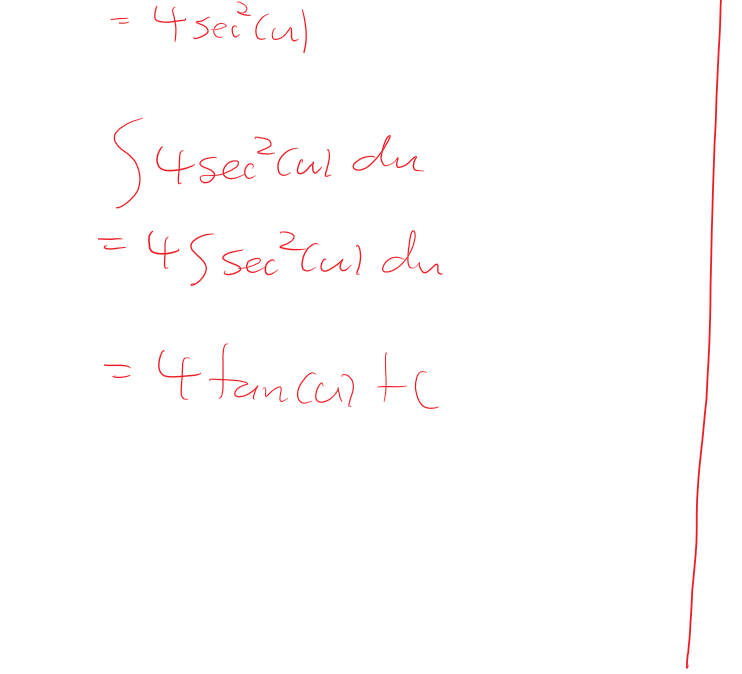 |
||||||||||||
|
|
|||||||||||||
|
|
|||||||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
|
|
|||||||||||||

![]()
Calc1231W5T3 - Integration by circle trig substitution
Friday, 24 August 2018
1:05 PM






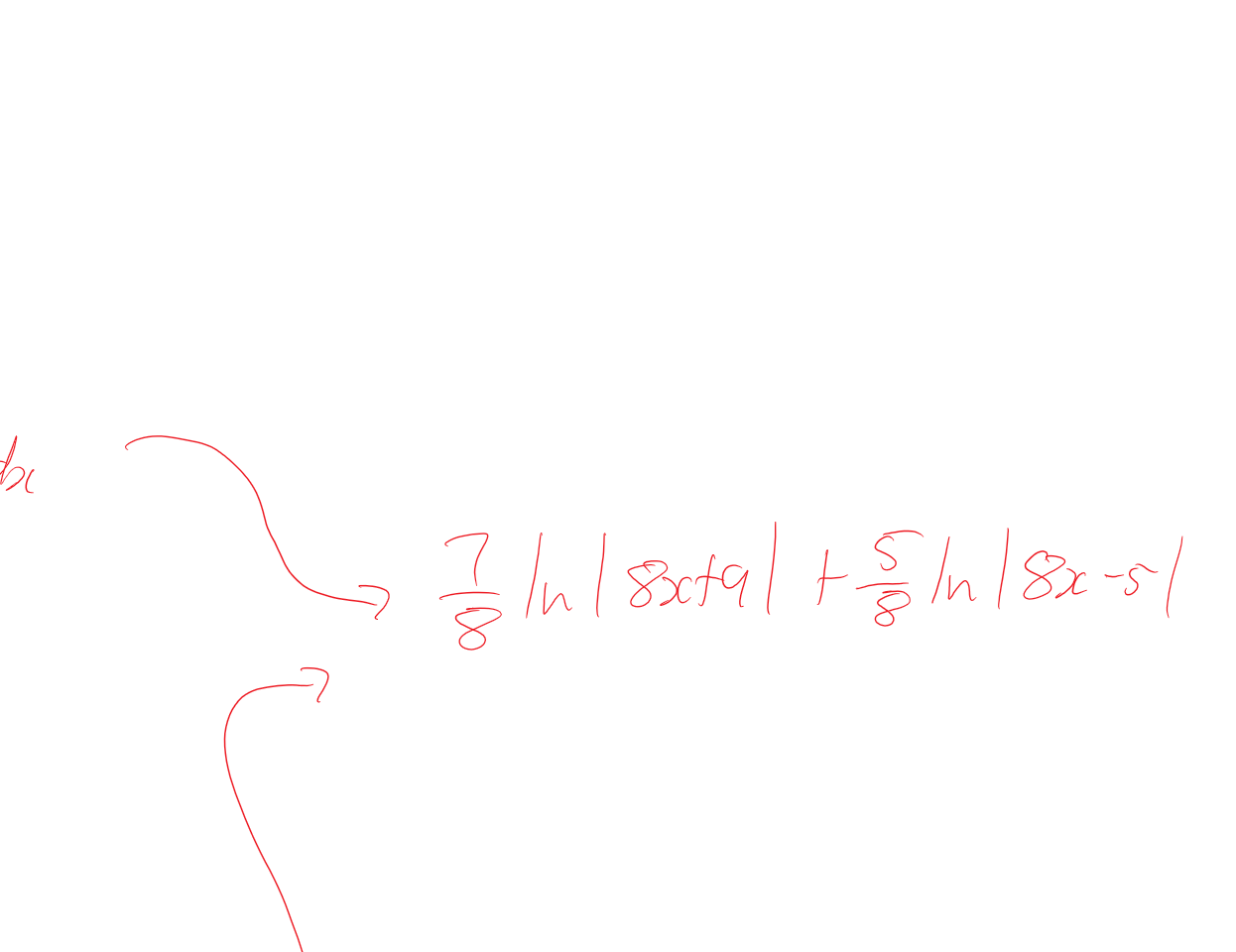


|
|
|||
|
|
 |
||
|
|
|
||
|
|
|
|
|||||||||||||
|
|
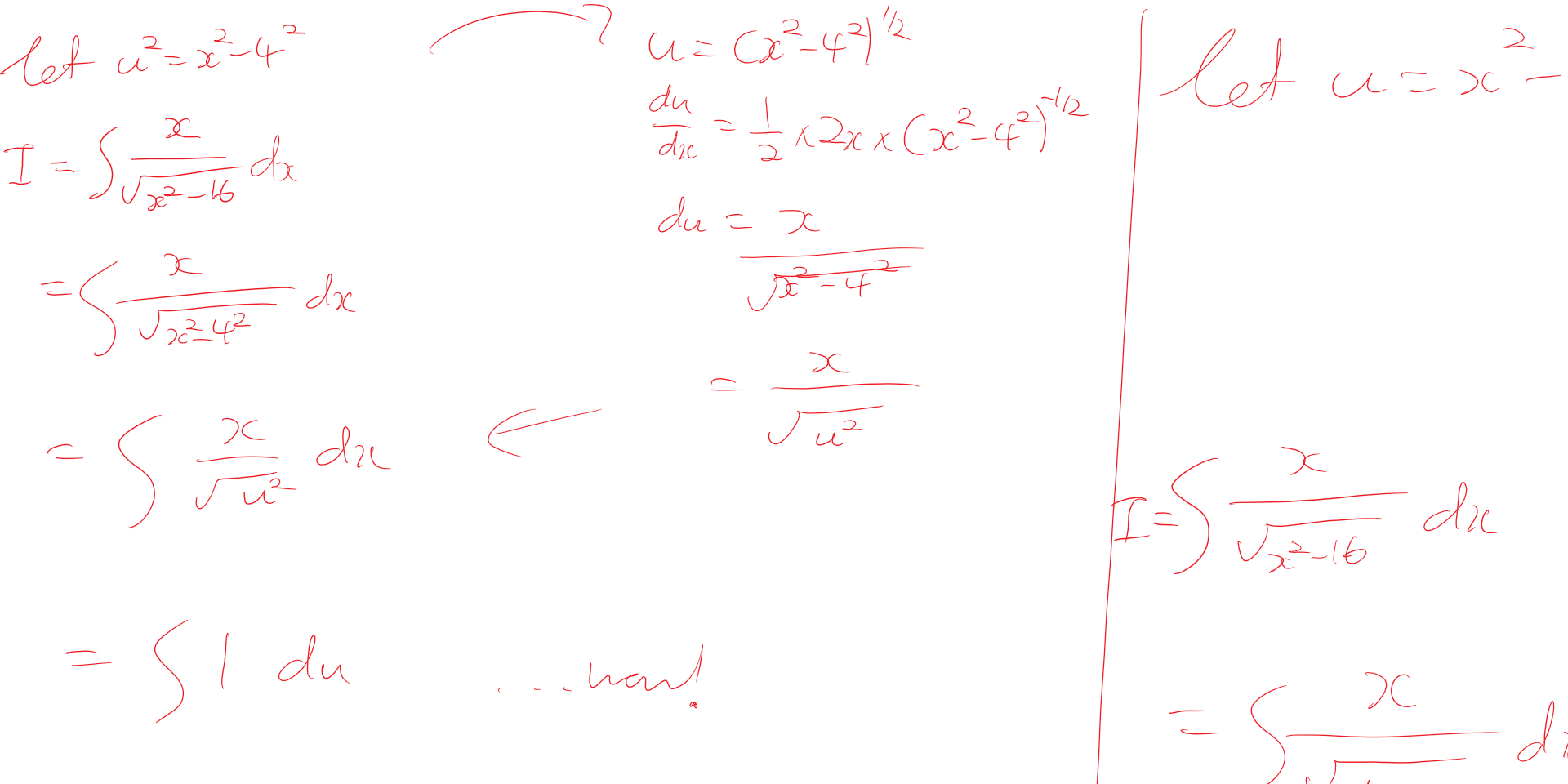 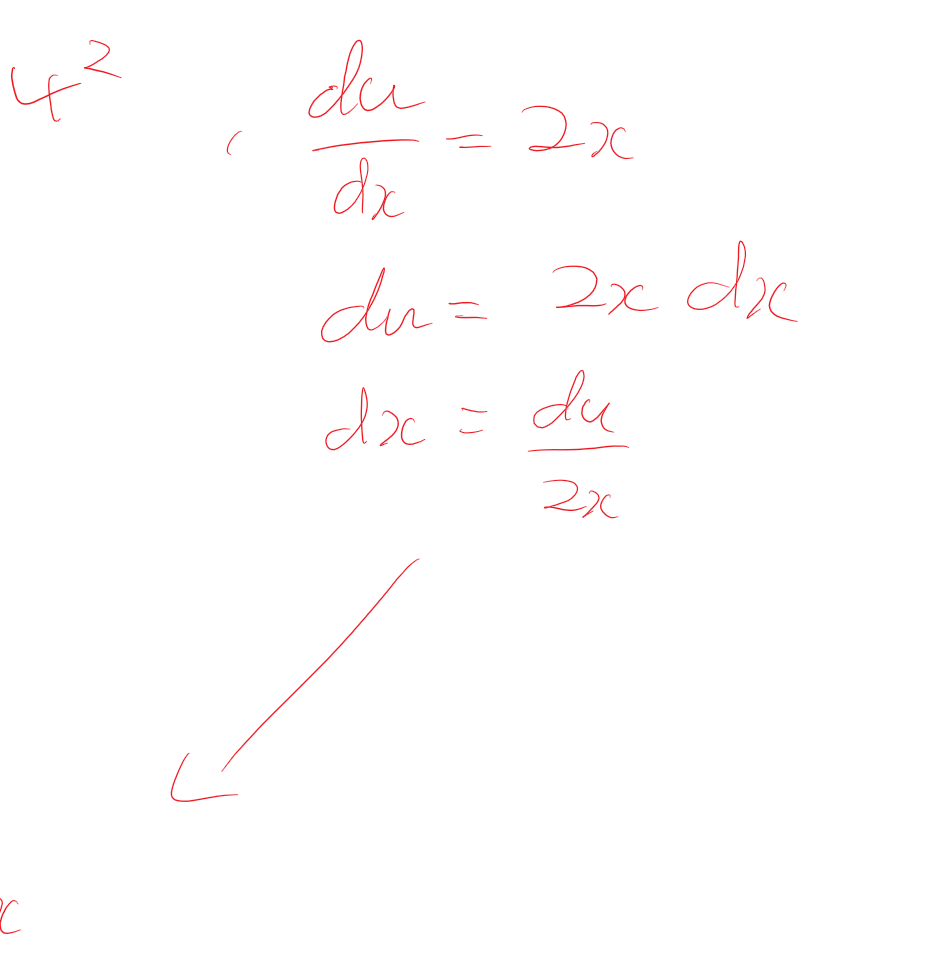 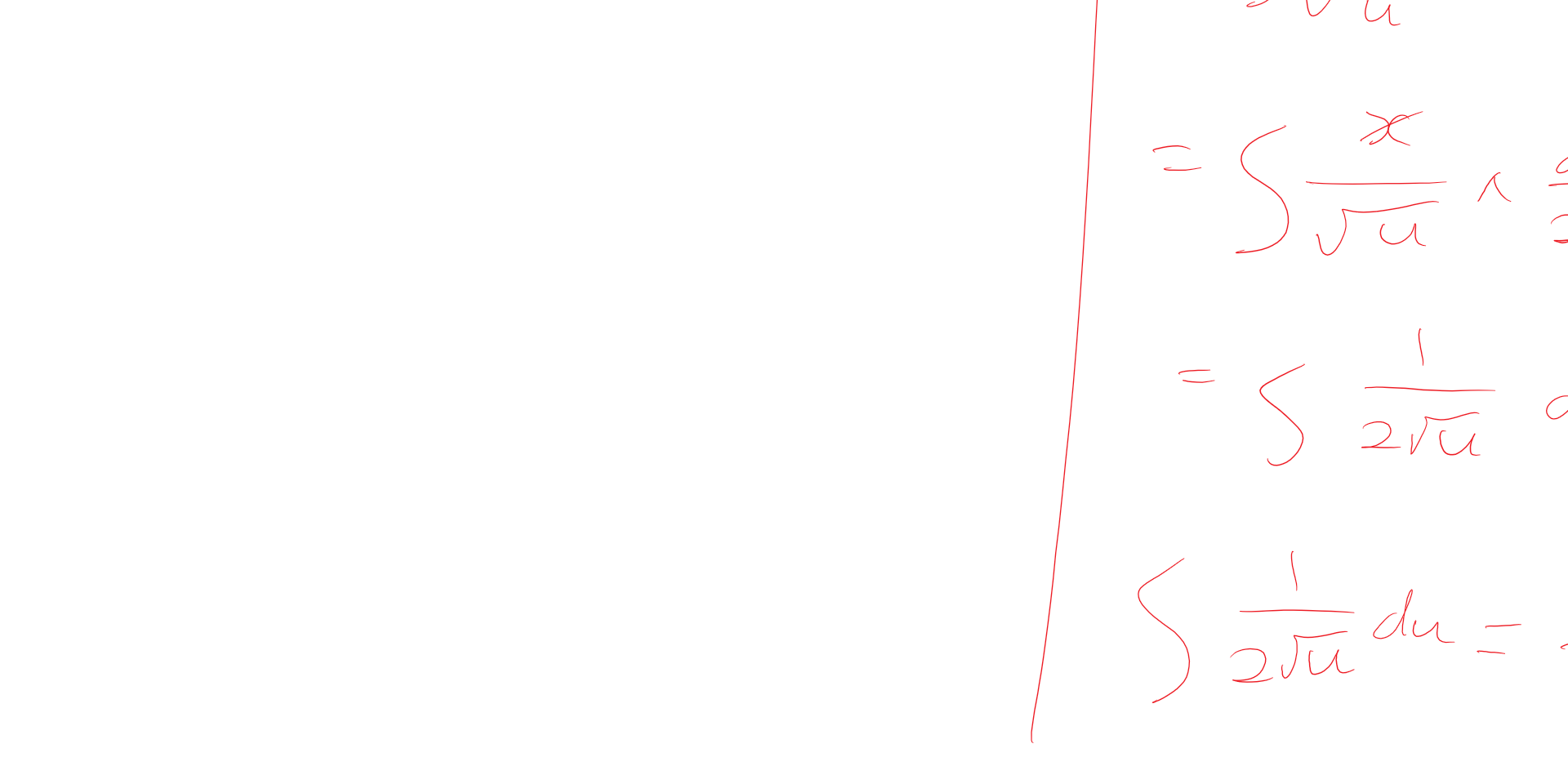 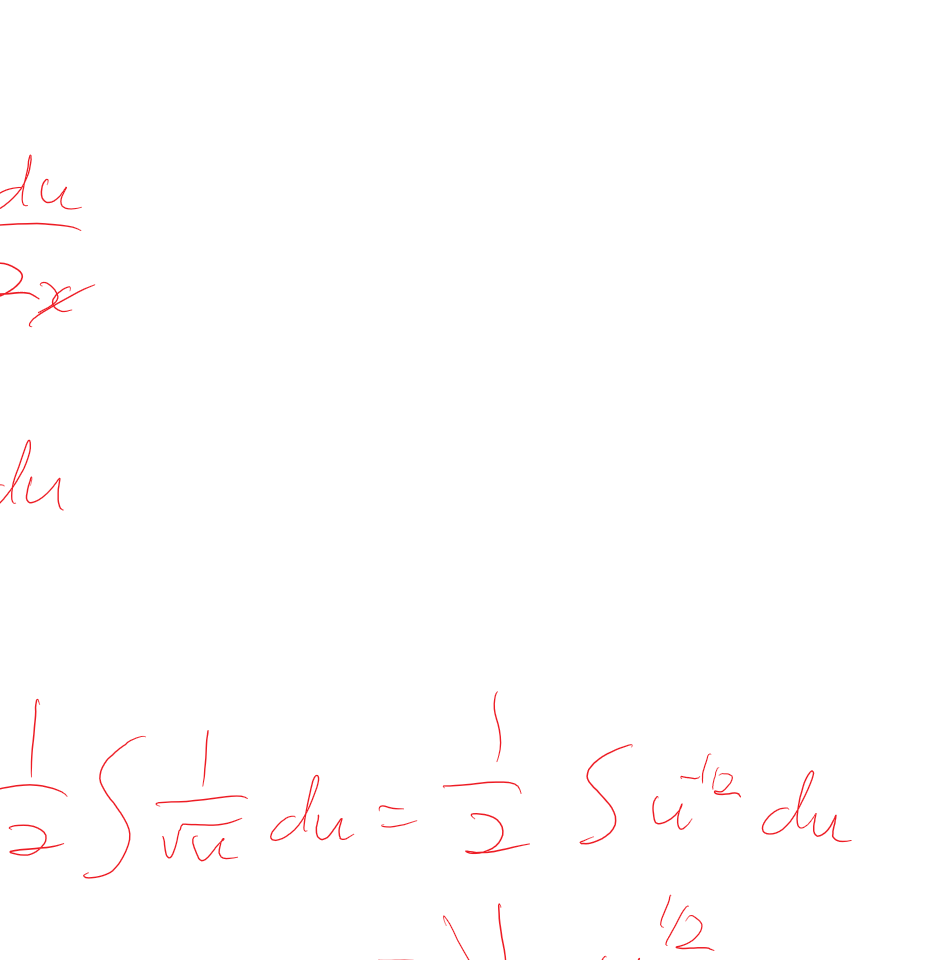  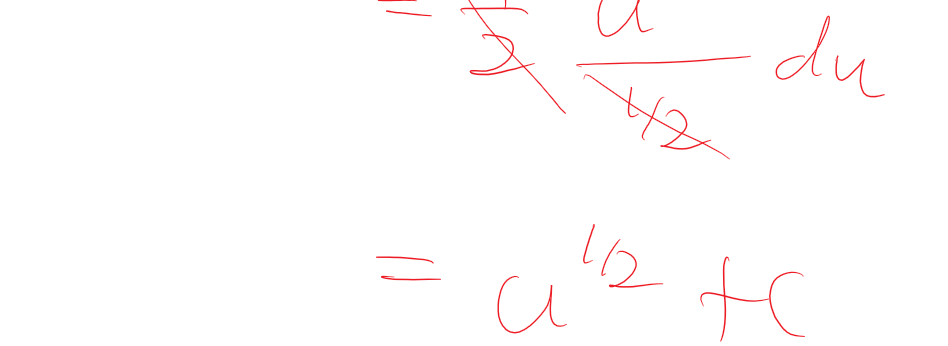 |
||||||||||||
|
|
|||||||||||||
|
|
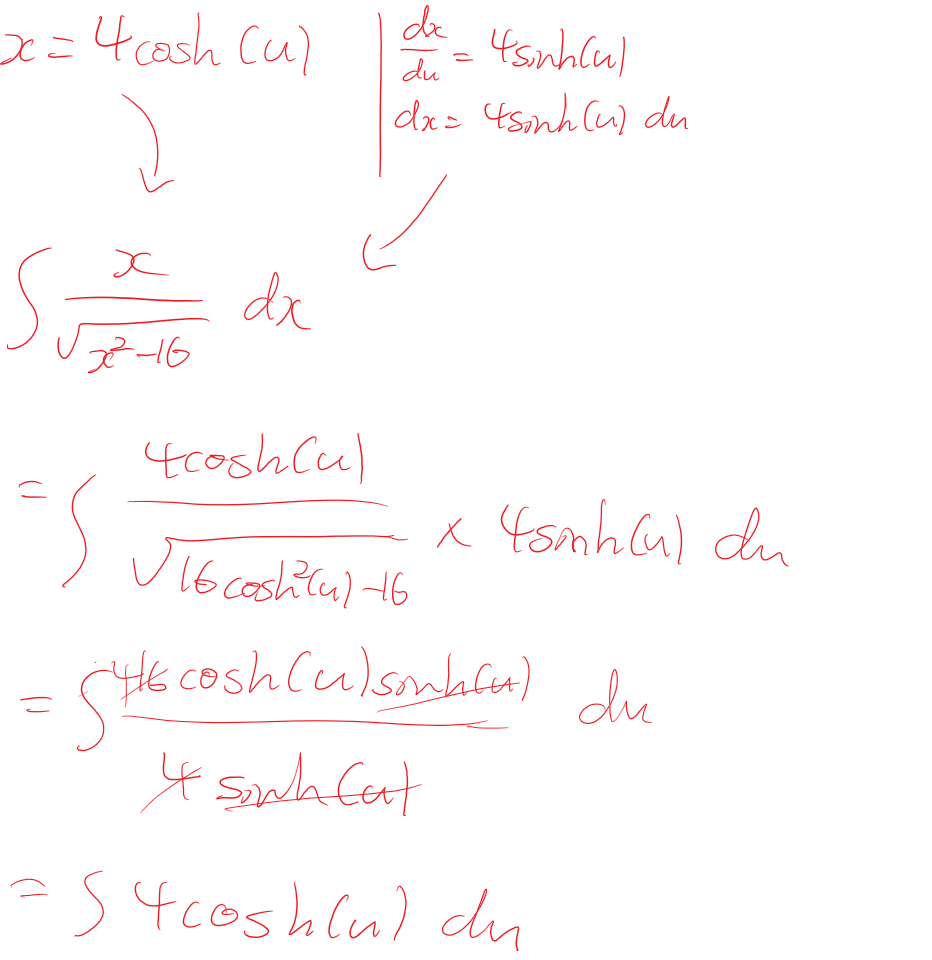 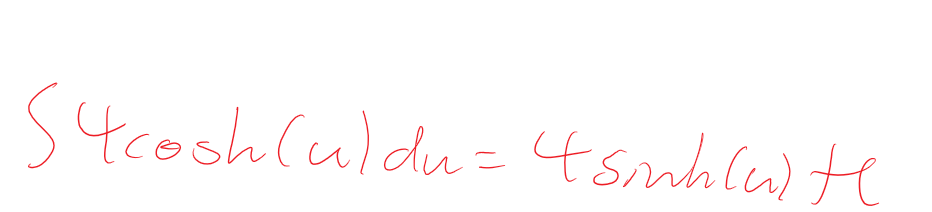 |
||||||||||||
|
|
 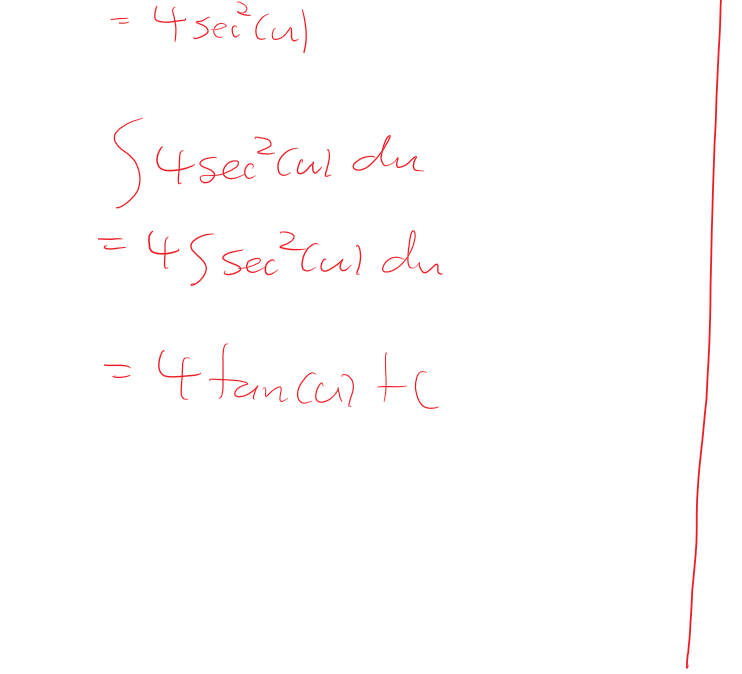 |
||||||||||||
|
|
|||||||||||||
|
|
|||||||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
|
|
|||||||||||||
|
|
|
||||||||||||
|
|
|||||||||||||

![]()
Created with Microsoft OneNote 2016.