Theorem

Wednesday, 5 September 2018

1:18 PM

The Taylor Polynomial of degree  for  at  is given by

 

 

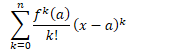
If  has  continuous derivatives on an open interval  containing , then for each

 

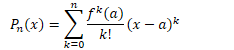
(Lagrange remainder)

 

This theorem says that we can approximate a function by its Taylor polynomial and with an error term

The error will depend on both the degree of the Taylor polynomial and the value of x.

The more terms, the better the approximation

The closer  is to , the better the approximation

 

 

• Taylor's theorem is a generalisation of the Mean Value Theorem