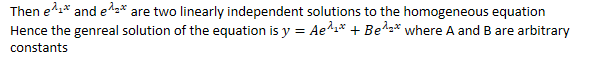Second Order Ordinary Differential Equations

Monday, 27 August 2018

10:34 AM

We consider an ODE of the form: ﷐﷐𝑑﷮2﷯𝑦﷮𝑑﷐𝑥﷮2﷯﷯+𝑎﷐𝑑𝑦﷮𝑑𝑥﷯+𝑏𝑦=𝑓﷐𝑥﷯
Where
𝑎 and 𝑏 are constants
𝑓(𝑥) is a given function

When 𝑓﷐𝑥﷯=0, we say that the ODE is homogeneous

We consider the homogeneous equation
﷐𝑦﷮′′﷯+𝑎﷐𝑦﷮′﷯+𝑏𝑦=0

Homogeneous Case
If ﷐𝑦﷮1﷯ and ﷐𝑦﷮2﷯ are solutions of ﷐𝑦﷮′′﷯+𝑎﷐𝑦﷮′﷯+𝑏𝑦=0
Then 𝑥 is 𝛼﷐𝑦﷮1﷯+β﷐𝑦﷮2﷯, where 𝛼 and 𝛽 are real numbers.

Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings
Ink Drawings

Theorem

The homogeneous equation hsas two linearly independent solutions and every solution is a linear combination of these solutions

Notes:

Two solutions and are linearly indepenent (they are not constant multiples of each other)
If and are linearly independent solutions, then every solution is of the form

Where and are constant

Solving

Try a solution of the form

Then ,

Substituting into the equation…

Since , then

satisfies the quadratic form - characteristic (auxiliary) equation

If then there are two real distinct roots

Let and be the roots of the characteristic equation and

Then and are two linearly independent solutions to the homogeneous equation
Hence the genreal solution of the equation is where A and B are arbitrary constants