Power Series // Radius of Convergence

Monday, 29 October 2018

2:11 PM

(Series of the form

(a - series of real numbers; power series in powers of

 

A function is said to be represented by a power series around  if there is and a sequence  such that

1.  converges whenever
2.  whenever RHS converges

 

The radius of convergence is the largest value of R

Radius of convergence is infinity if the series converges for all

Radius of convergence is zero if the series converges only for

Open interval is from  to

 

 

 

 

 

--

Consider

 

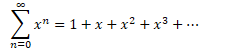
This is a power series (geometric) of the form  where ,

The geometric series converges for  and diverges for

 

So, the series  converges whenever

So, the radius of convergence is 1

Open interval of convergence is  to

 

 

Consider

 

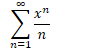
 Apply the ratio test for absolute convergence

 

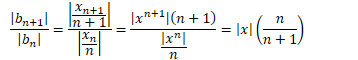
By the ratio test, the series converges absolutely by