Vector Spaces
Monday, 30 July 2018
12:35 AM
Matrices can be transformed into vectors
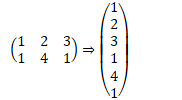
However, we lose the ability to perform matrix multiplication
Definition of a Vector Space
A vector space over the set of scalars is a non-empty set of objects called vectors,
for which addition andd scalar multiplication are defined are obey the axioms:![]()
- Closure under
Addition

- Associative Law of
Addition

- Commutative Law of
Addition

- Existence of
Zero

- Existence of a
Negative
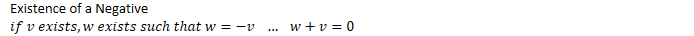
- Closure under Scalar Multiplication

- Associative Law of
Multiplication by a Scalar

![]()
- One vector
![]()
- Scalar
Distributive Law

- Vector
Distributive Law

To prove that something is (not) in a vector system, use a real vector that matches/violates the axioms
Approaching Vector Space Questions
- Write the hypothesis at the beginning
- Write the conclusion at the end
- Fill in the arguments