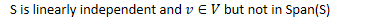Terminology

Thursday, 16 August 2018

5:42 PM

Vector Set

Subset

Spanning Set -  Every vector in V is a linear combination of B, has solutions

Subspace

Linearly Independent Set -  Every vector in span(B) can be uniquely written as a linear combination of B

• 
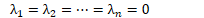
• Only one solution
•  has a unique solution
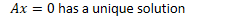
• All columns of  are leading

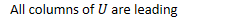
Linearly Dependent Set -

• Infinite solutions
• Some columns are non-leading

PROPER subspace?

 

 

 

Let  be a finite non-empty set of vectors in a vector space .

1.  is a vector which can be written as a linear combinatio of S
   Values of scalars n the linear combination are unique iff S is linearly independent
2. S is linearly independent iff no vector can be written as a linear combination of the other vectors of S.
3. For any , we have  iff
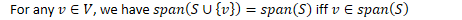
4. Span of every proper subset of a proper subspace of span(S) iff S in linearly independent
5. S is linearly independent and  but not in Span(S)