Rank-Nullity Theorem

Monday, 27 August 2018

9:36 AM

Let  be an  matrix. Suppose that the columns of A are  and  reduces to a row-echelon form matrix

 

1.  is the solution set of
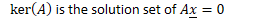
2. A basis for  is a basis for the solution set of
3. The dimension of the solution set is the number of (independent) parameters used in the solution
   That is,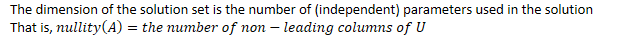
4. The  is the set of all vectors of the form
   Hence,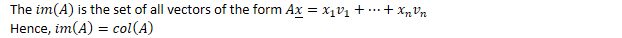
5. A maximal set of linearly independent columns of  forms a basis for .
   The set of vectors which are columns of  corresponding to the leading columns of  is a basis for

 

Rank-Nullity Theorem:

If  is an  matrix, then

 

If  is reduced to row-echelon form .

 = number of leading columns of .

 = number of non-leading columns of .

 = number of columns of  = number of columns where

 

Therefore  columns of  -

Therefore  columns of  -