Week 8 - Counting and recurrence
Tuesday, 9 April 2019
10:43 PM
|
|
|||
|
|
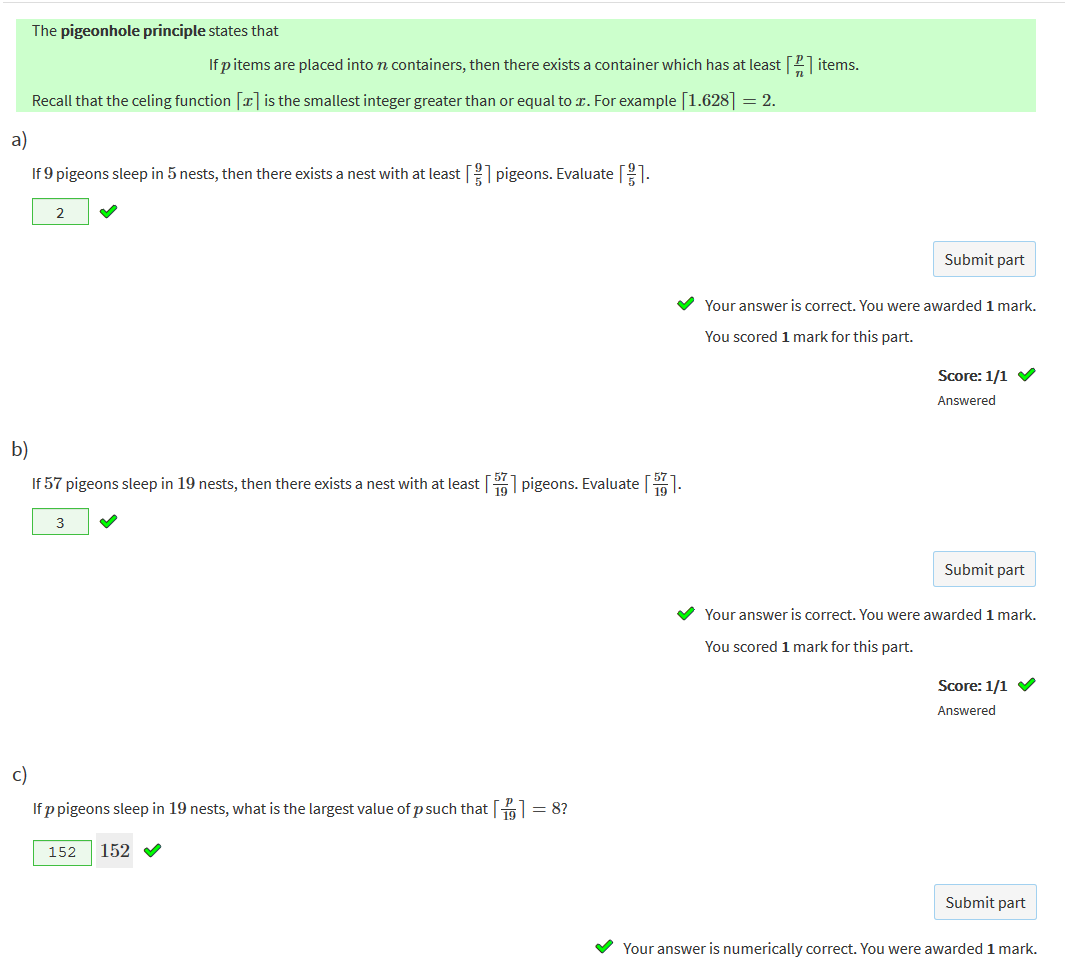
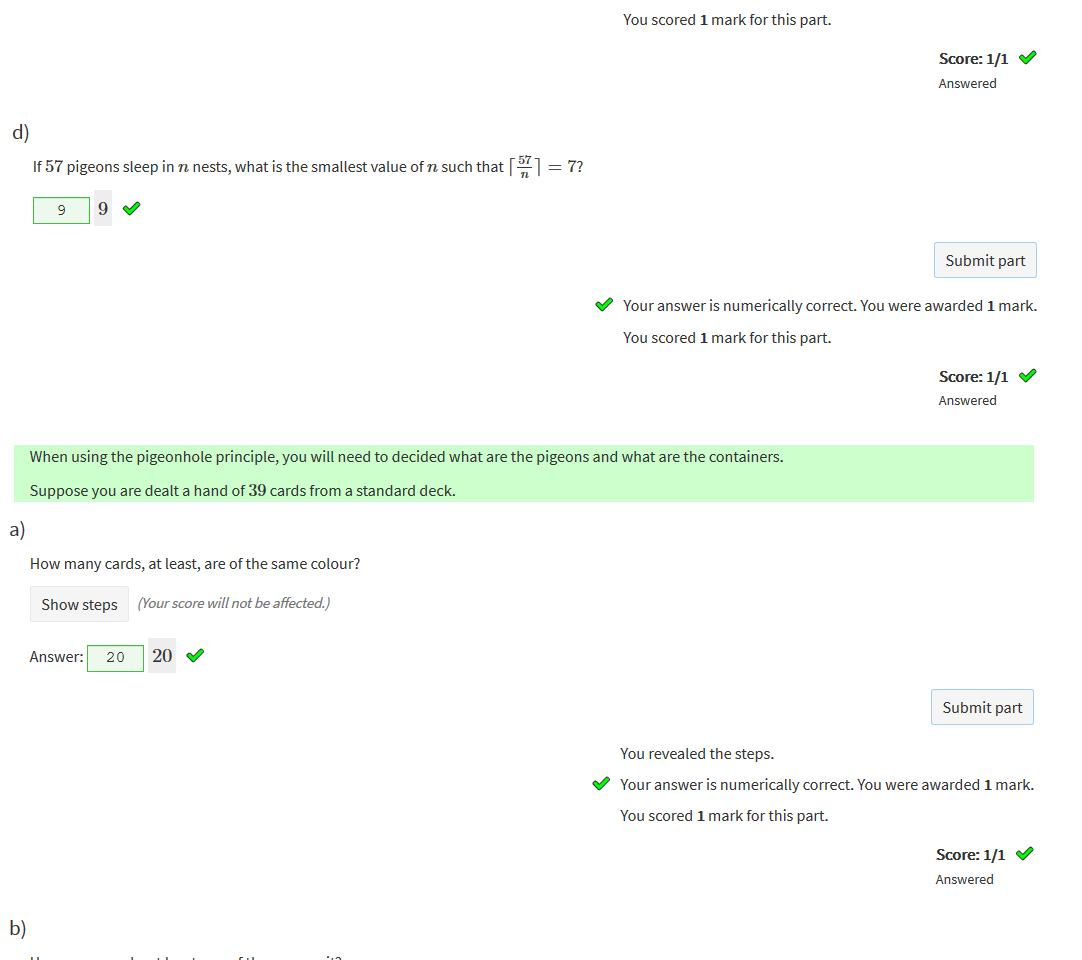
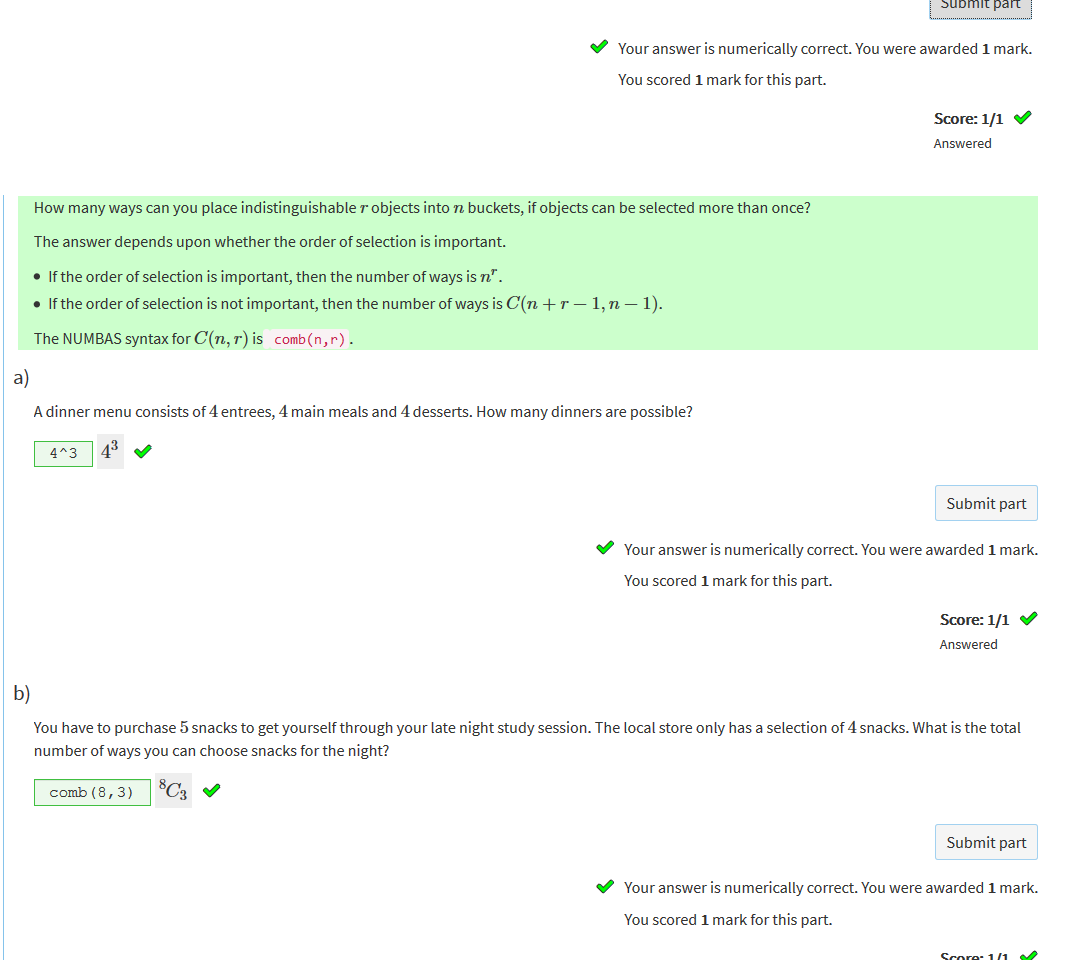
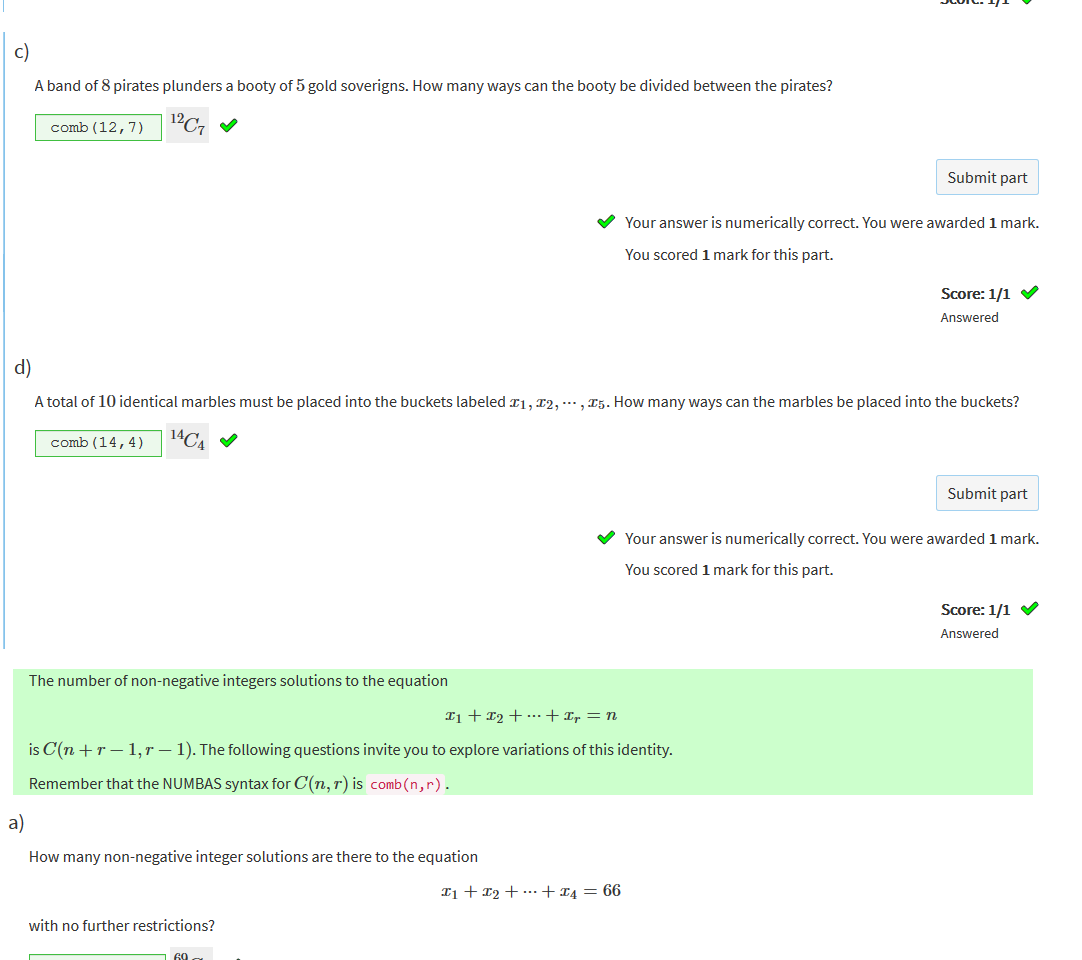
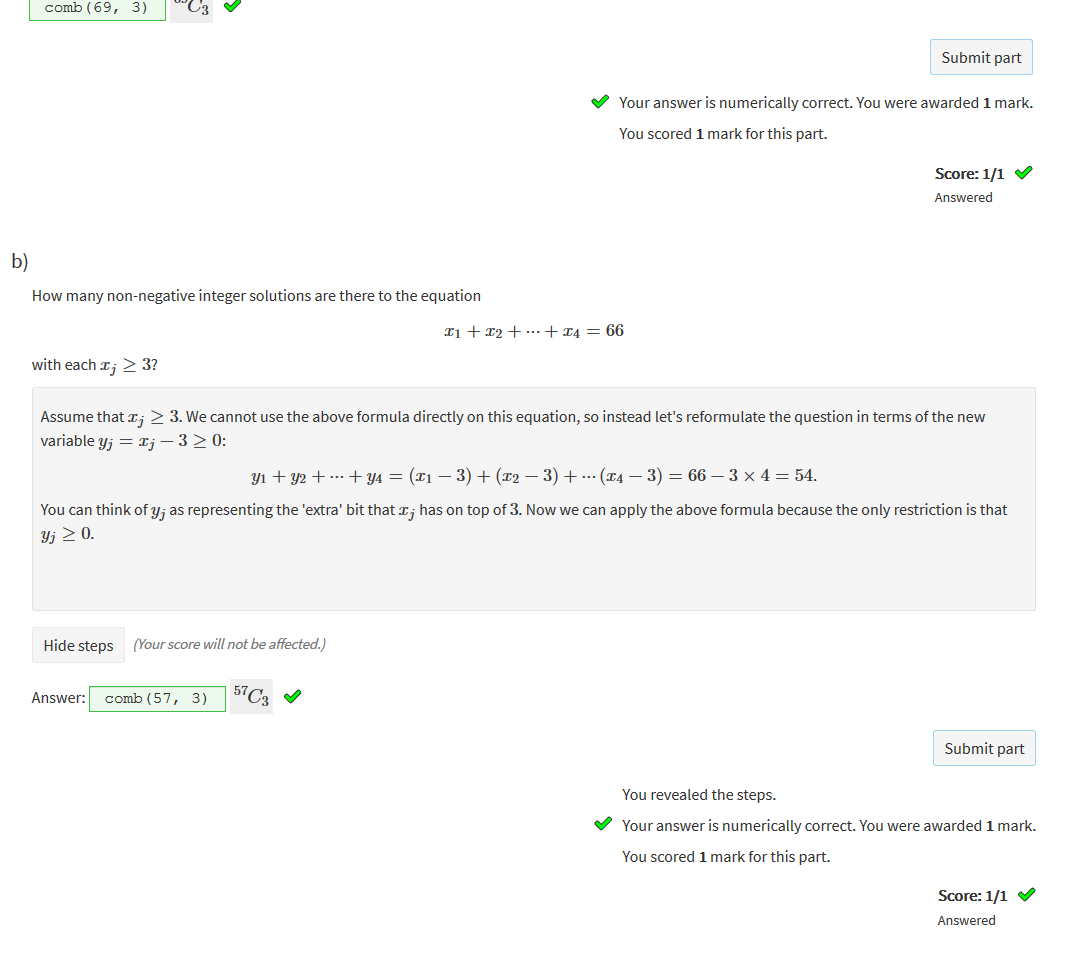
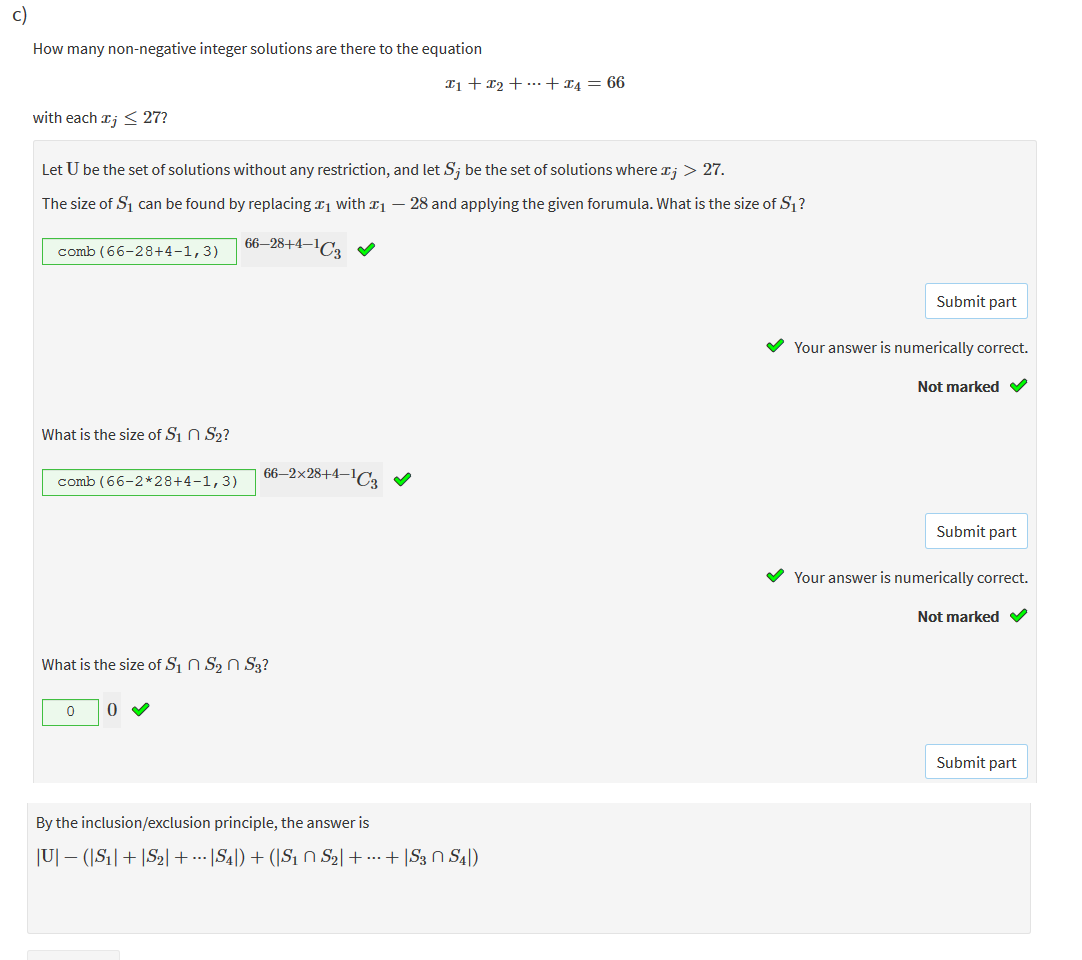
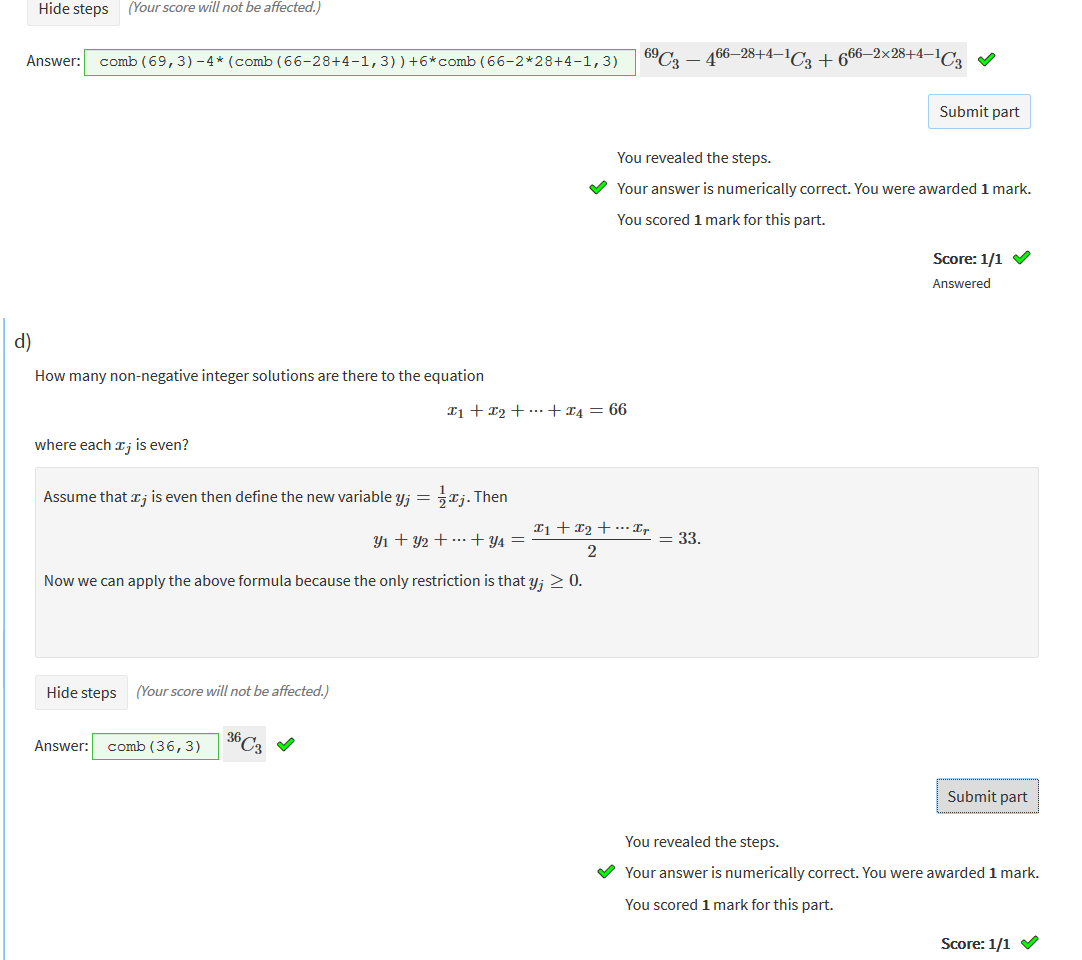
n is the container r is the amount |
||
|
|
          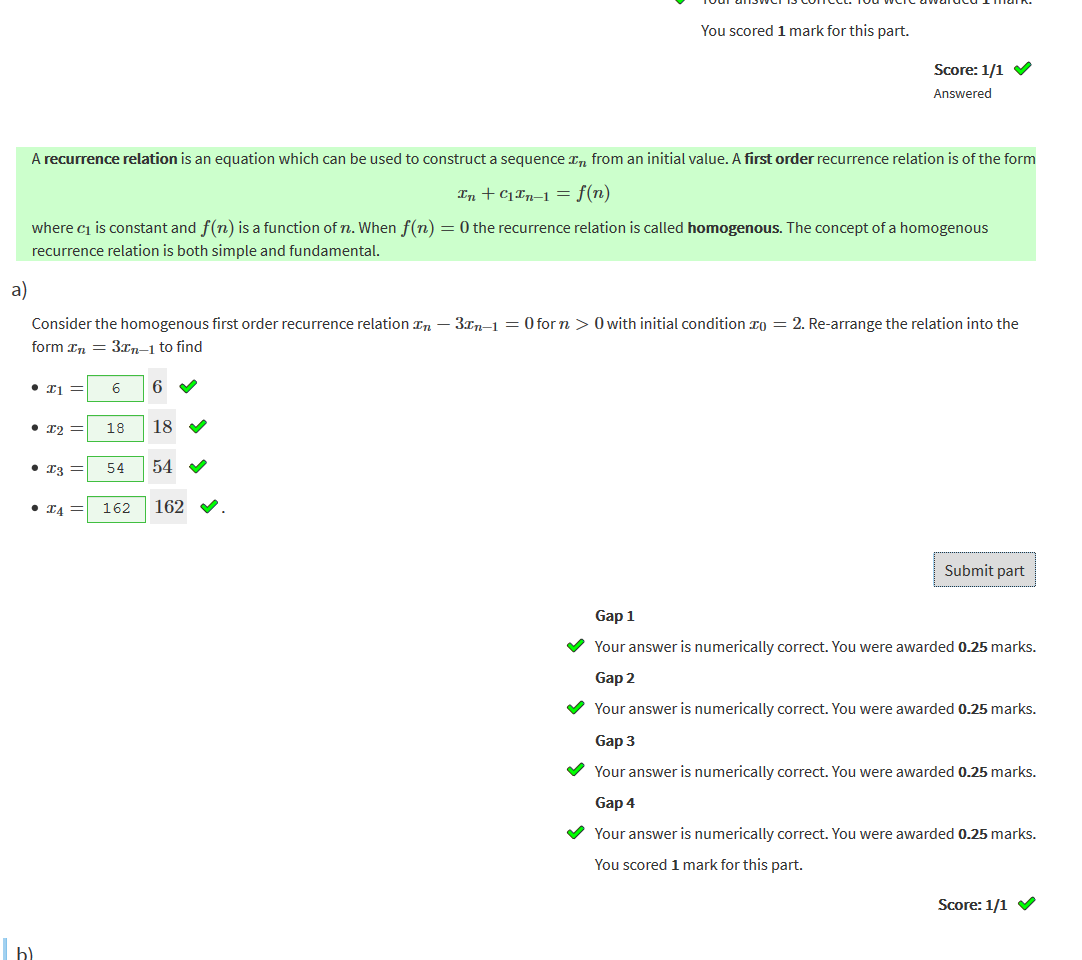 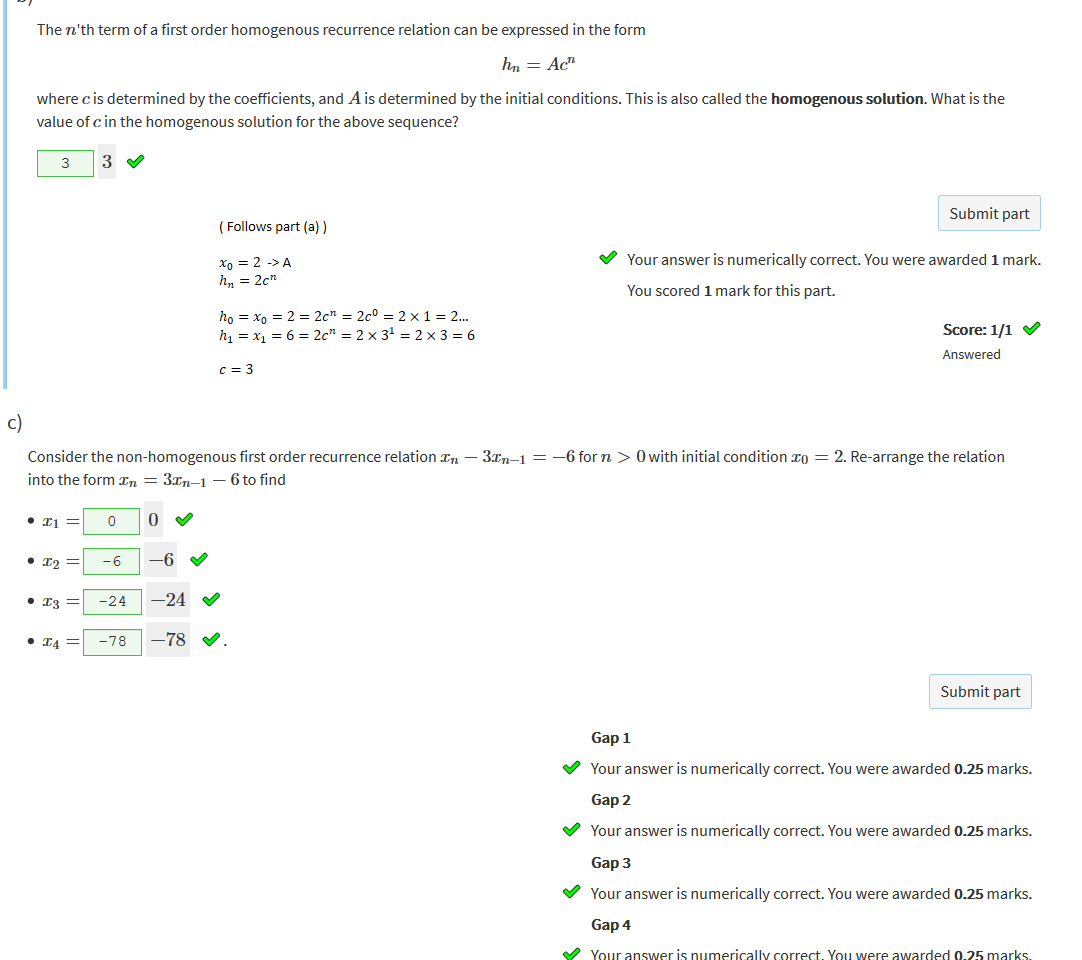 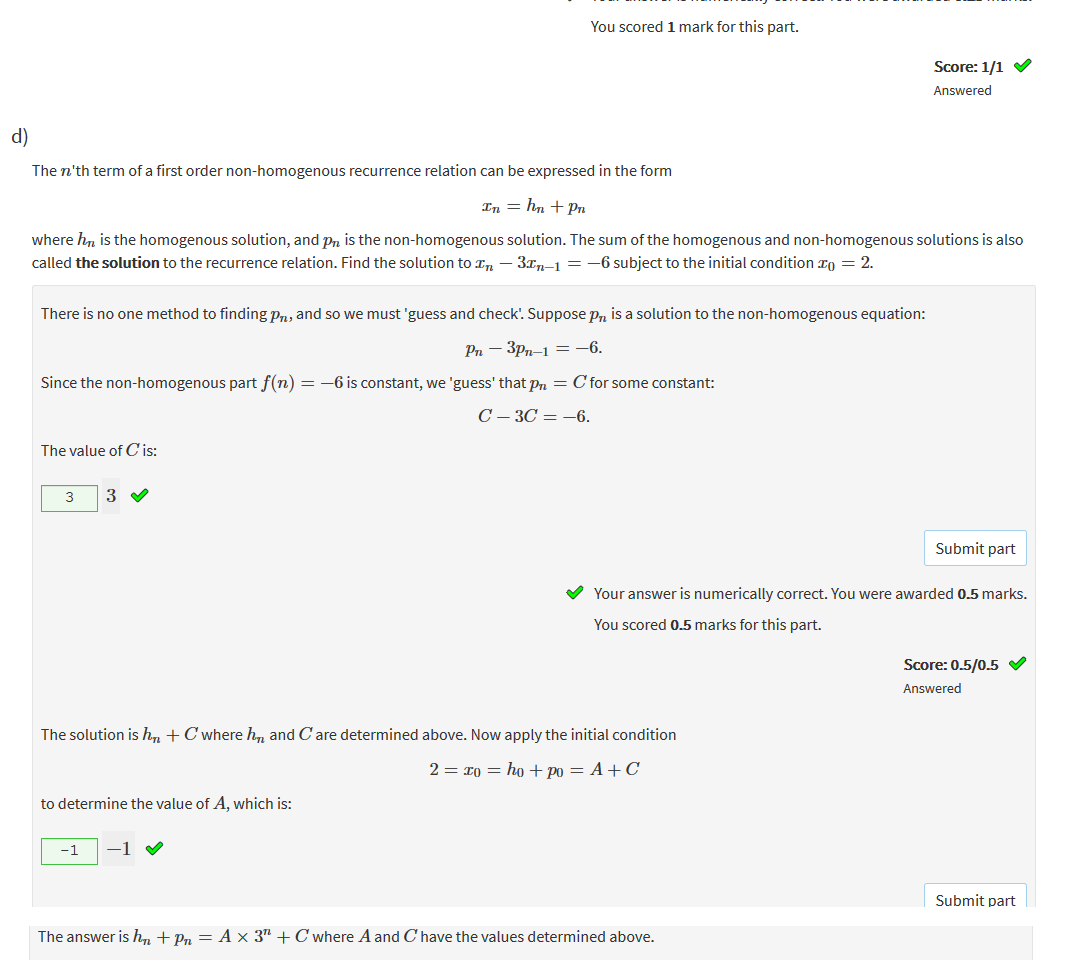 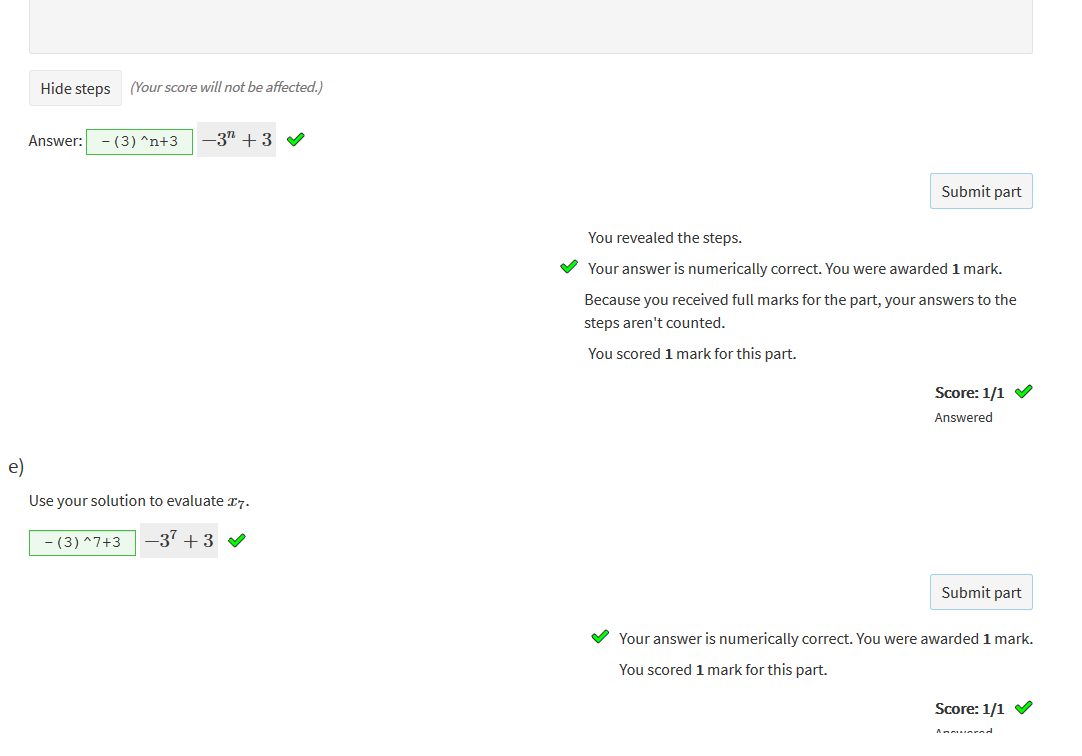 |
||
|
|
Week 8 - Counting and recurrence
Tuesday, 9 April 2019
10:43 PM
|
|
|||
|
|
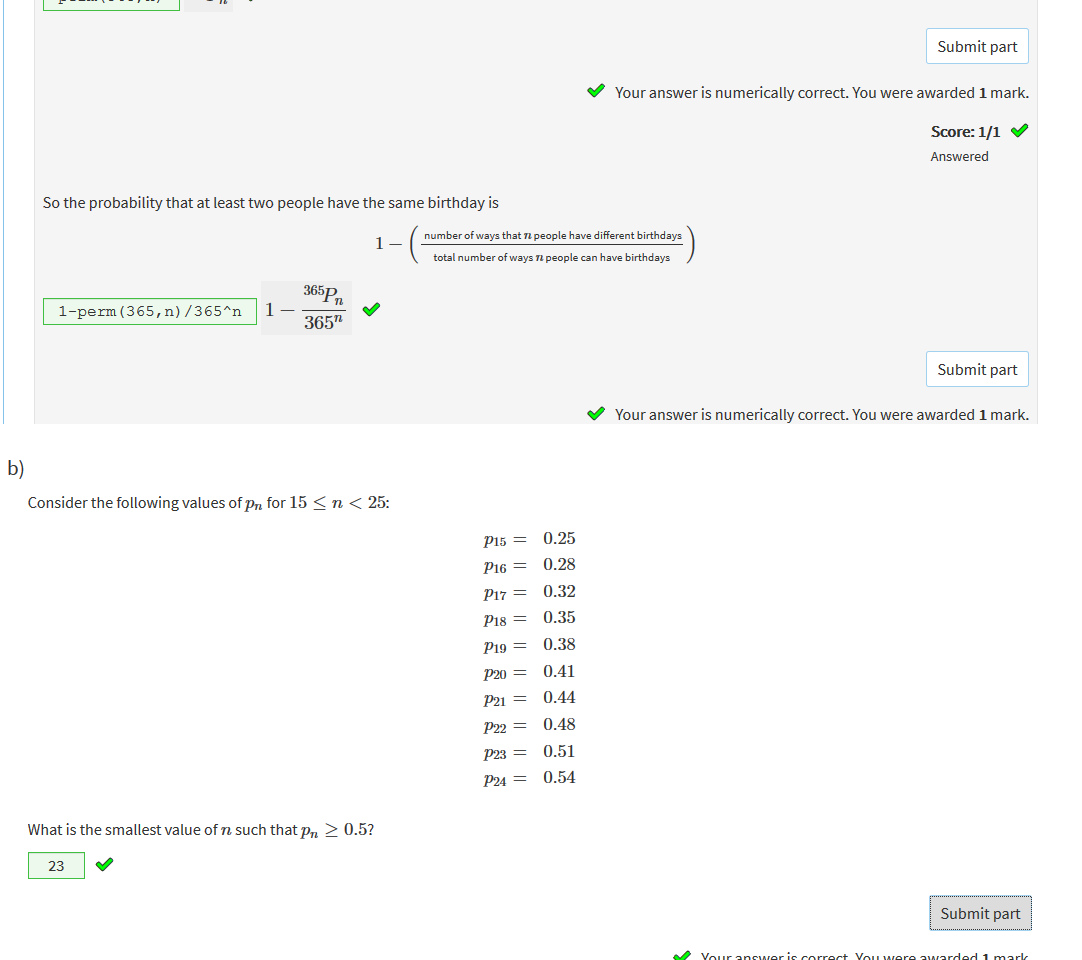
n is the container r is the amount |
||
|
|
              |
||
|
|
Created with Microsoft OneNote 2016.