L1 - Definitions

Sunday, 17 February 2019

3:55 PM

A set is a collection of well-defined distinct elements (discard any duplicates)

( in  where )

 

 - elem in set

 - elem not in set

 

The cardinality of a set,  is the number of elements in .

 

---

 

 - natural numbers | 0,1,2,3

 - integers (whole numbers) | - 3,-2,-1,0,1,2,3

 - fractions (rational numbers) | -1,0,1,2,1/2,3,1/3,2/3

 - real numbers (everything)

 - complex numbers (everything + complex)

 

---

 

Two sets are equal () if every element of  is in , and every element of  is in .

The empty set (?) is a set which has no elements. But it is still a thing!

 

---

 

A subset of a set is a part of a set.

 

A proper subset is a subset which is not equal to the original set (things actually taken out)

 

The power set  is the set of all subsets of .

 and

 and

 

The number of subsets of  is

// Subset -> remove one set of brackets and check if it is an element

 

The universal set is the scope of items in a set, for difference, complement etc

Complement (c, ) - not

Difference (-, \) - but not

Union () - or

Intersection () - and

 

Two sets are disjoint if

 

• Inclusion-Exclusion Principle -

 

 

---

 

 

 

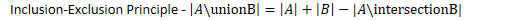
The Cartesian Product

When  and  are small finite sets, we can use an arrow diagram to represent a subset  of

 

 

---

 

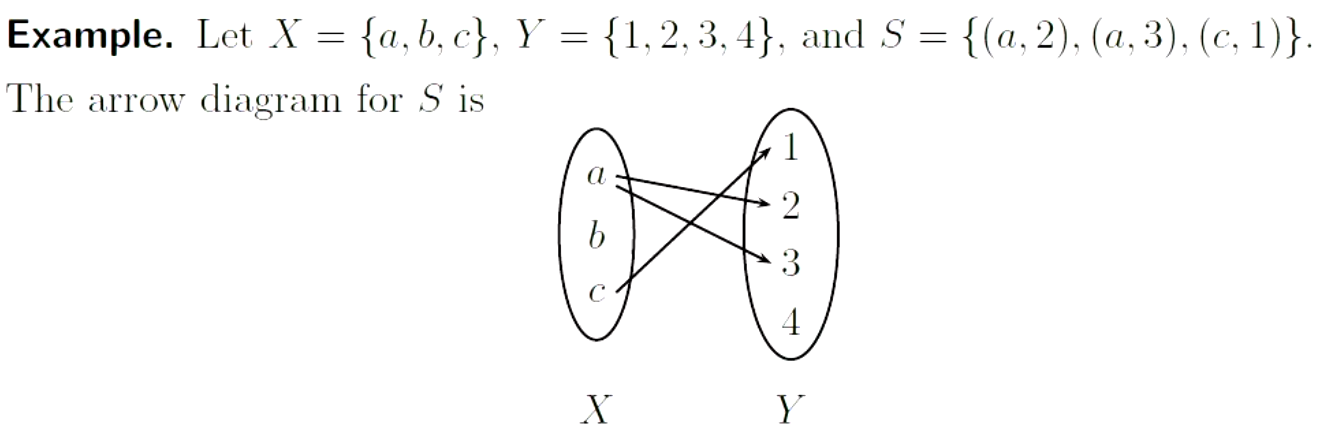
A function  from a set  to a set  is a subset of  so that for every  there is exactly one  for which  belongs to

 

 " is a function from  to "

 is the domain of f

 is the codomain of x

 

The set of values  produced by  is called the image (of  under  // value of  at )

The range of  is the set of produced values of

The range is the image of x under f

 

The inverse image of  is the set of inputs of  which have an output

 

 

// What's not a function?

Several outputs for the same input

No output for a possible input

---

 

 

 

 

 -   Largest integer smaller than

 -  → Smallest integer larger than

 

If a function is injective (one-to-one), each output is produced by only one input

Proof Usage: , then

 

For a given function…

The set of possible inputs  is called the domain

The set of possible outputs  is called the codomain.

The set of actual outputs is called the range.

 

Actual Outputs: A function must be defined for every element of its domain, but the codomain may contain additional elements that are unused

 

A function is surjective (onto) if the codomain and range are equal.

(Everything in the codomain is in the range)
Proof Usage: If a function is surjective, then every element of the codomain exists

 

A function is bijective if it is both injective and surjective.

This guarantees that  has an inverse function

 

For each

Injective - at most one

 

Surjective - at least one

Bijective - exactly one