The Dirac Delta

Monday, 25 March 2019

4:21 PM

Consider a pulse, a signal that is non-zero only over a short time

Ink Drawings Ink Drawings Ink Drawings Ink Drawings      

 

 

 Now send 𝜏→0, while preserving its energy Dirac delta (impulse) 𝛿﷐𝑡﷯===﷐﷐lim﷮τ→0﷯﷮﷐Π﷮𝜏﷯(𝑡)﷯=﷐﷐+∞, 𝑡=0﷮0,𝑡≠0﷯﷯ Such that ﷐−∞﷮∞﷮𝛿﷐𝑡﷯ 𝑑𝑡﷯=1 Used in a functional sense, to map from a function to a value ﷐∞﷮∞﷮𝑓﷐𝑡﷯𝛿﷐𝑡−𝑎﷯ 𝑑𝑡﷯=𝑓﷐𝑎﷯ (just 𝑓﷐𝑎﷯) "samples" 𝑓(𝑡) at 𝑡=𝑎 Fourier Transformation of 𝛿﷐𝑡﷯ ℱ﷐𝛿﷐𝑡﷯﷯=﷐−∞﷮∞﷮𝛿﷐𝑡﷯﷯﷐𝑒﷮−𝑗𝜔𝑡﷯ 𝑑𝑡=1 Sample ﷐𝑒﷮−𝑗𝜔𝑡﷯ at 𝑡=0 𝛿﷐𝑡﷯=𝛿﷐𝑡−0﷯ So ﷐𝑒﷮−0𝜔𝑡﷯=1 So then Ink Drawings Ink Drawings Ink Drawings Ink Drawings  a   

 

                     

                     

 

 

 

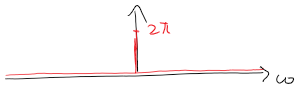
Ink Drawings Ink Drawings Ink Drawings  Ink Drawings Ink Drawings Ink Drawings Ink Drawings Ink Drawings

 

If we use the convolution operation, if we set  to  then

The output of an impulse into a system is the transfer function

How to generate an impulse?

Square wave with a low duty cycle

 

TL;DR

We can use an impulse to characterise a circuit or system

 

The impulse in the frequency domain is purely DC (only at )

 

Created with Microsoft OneNote 2016.