Fourier Series

Thursday, 28 February 2019

1:33 PM

The Fourier Series gives us the ability to represent any waveform as a series of sinusoids.

This therefore allows phasor analysis on any waveform (Phasor analysis required a sinusoid)

 

Given a real function , periodic with period

 

Such that

 : "fundamental frequency"

 

Represent a function

• We can break the signal into its frequency components
• DC ()
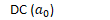
• And real value sin/cosine

 

 

The Fourier series represents  as a DC component and an AC component comprising an infinite series of harmonic sinusoids

 

If the Dirichlet conditions are satisfied, then the Fourier series will converge:

1.  is single-valued everywhere (one output)
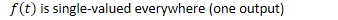
2.  has a finite number of discontinuities in any one period
3.  has a finite number of maxima and minima in any one period
4. 

 

 

 

 

 

 

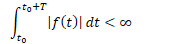
For practical signals, how do we find the Fourier series representation.

 

 

 

 for

 

 for

 

 for

 for

 

 generalises to

 

Integrate

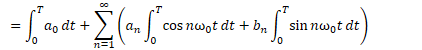
// identity = 0

 

 

Now multiply by  and integrate

 

 

 

Multiply by  and integrate