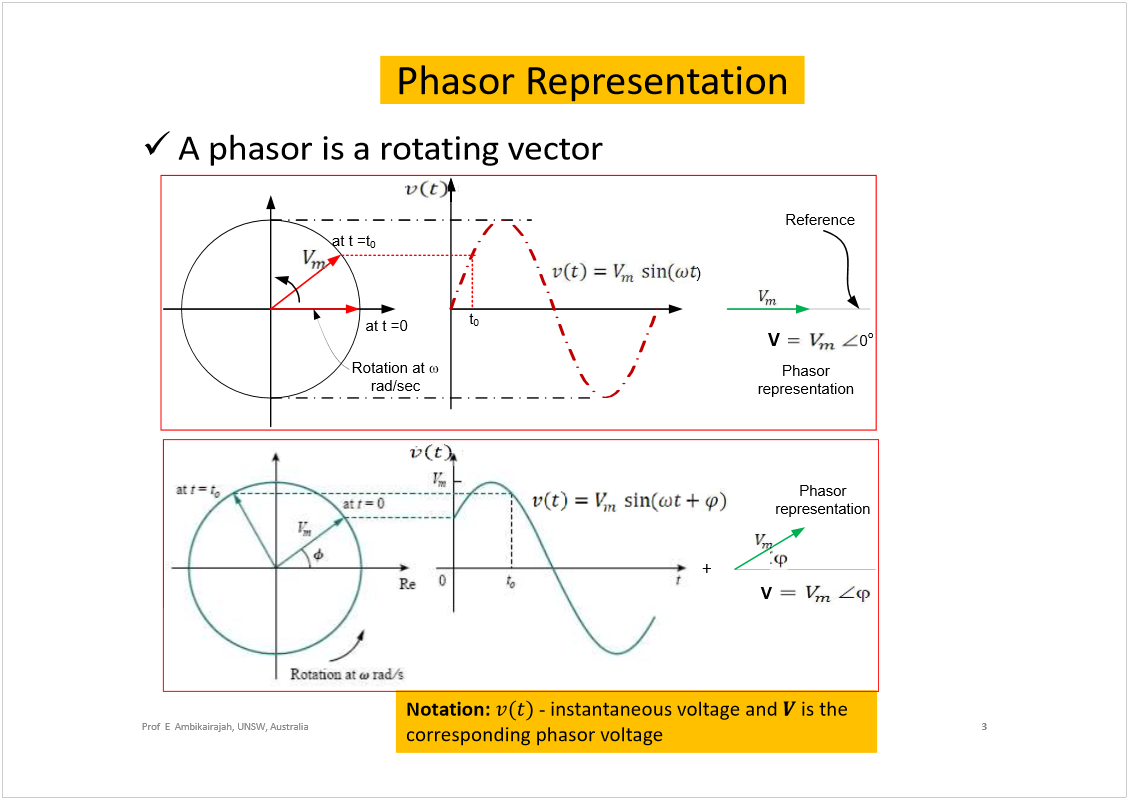
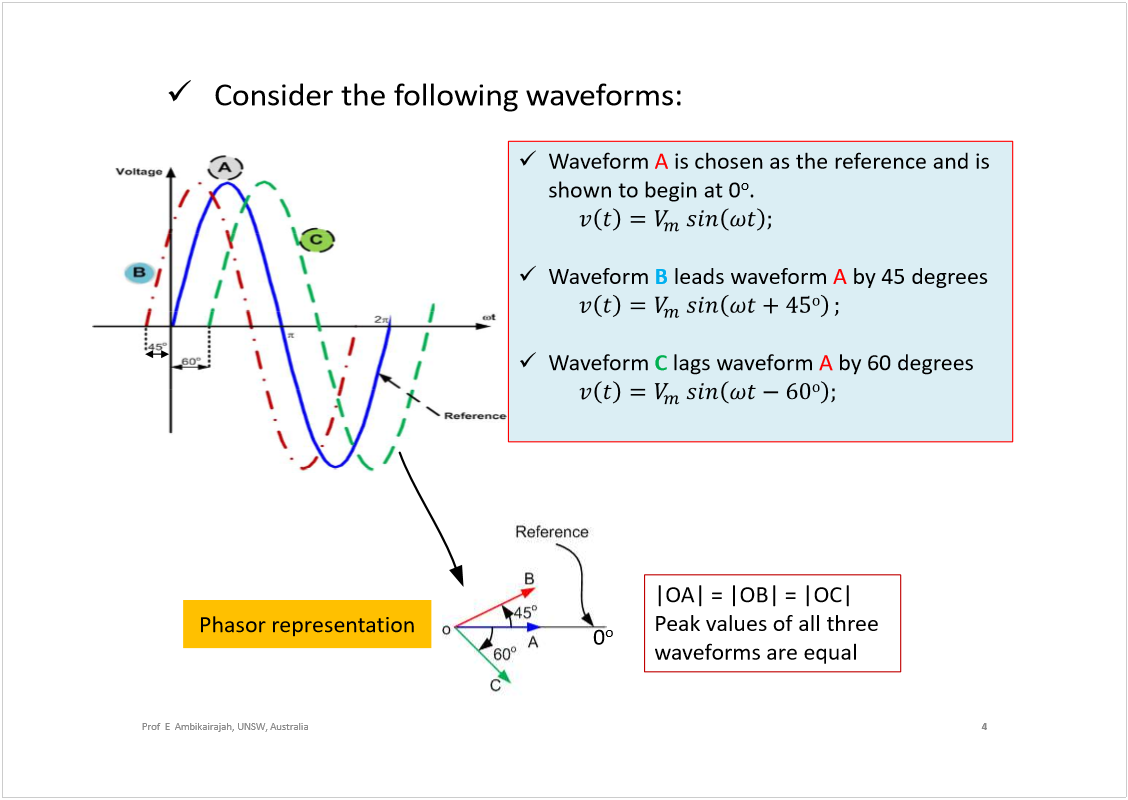
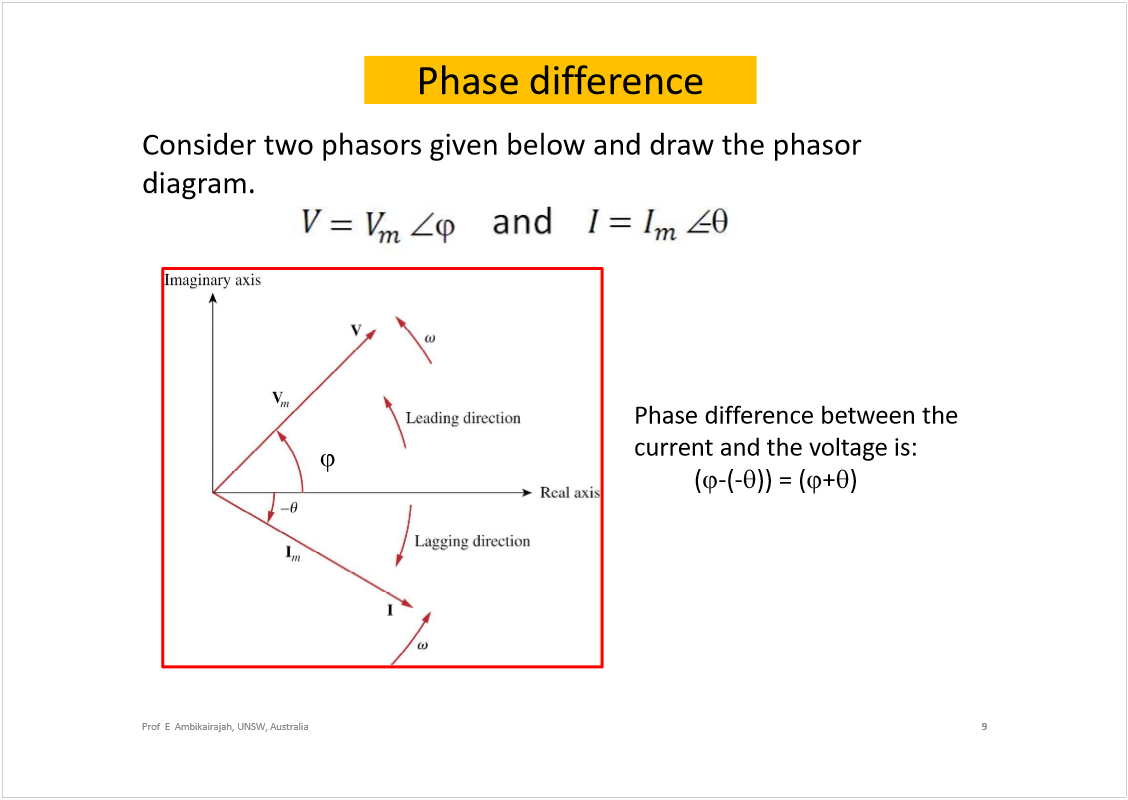
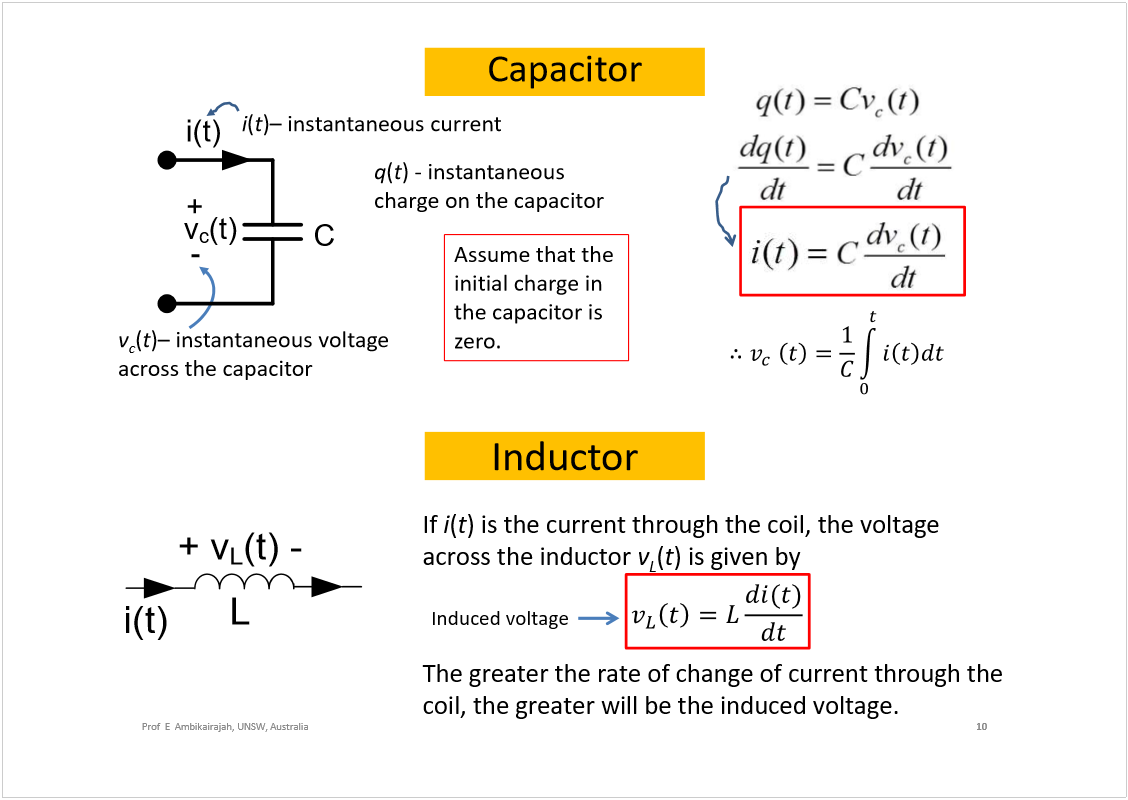
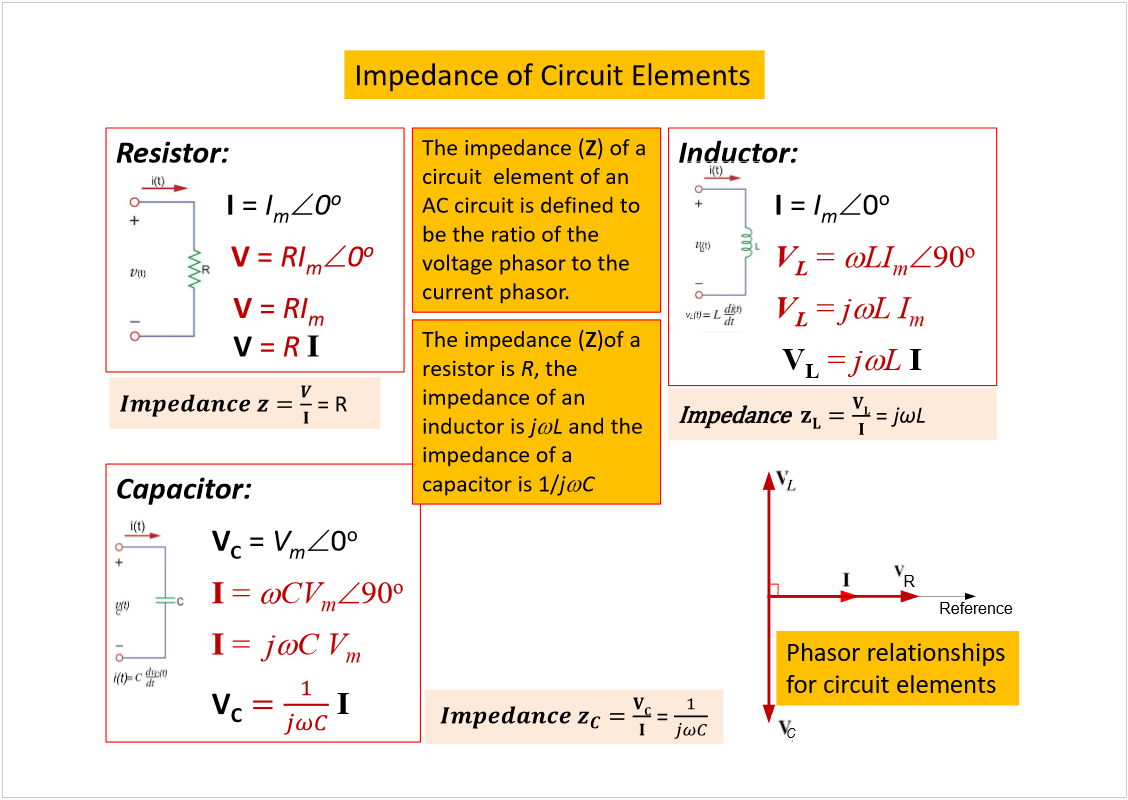
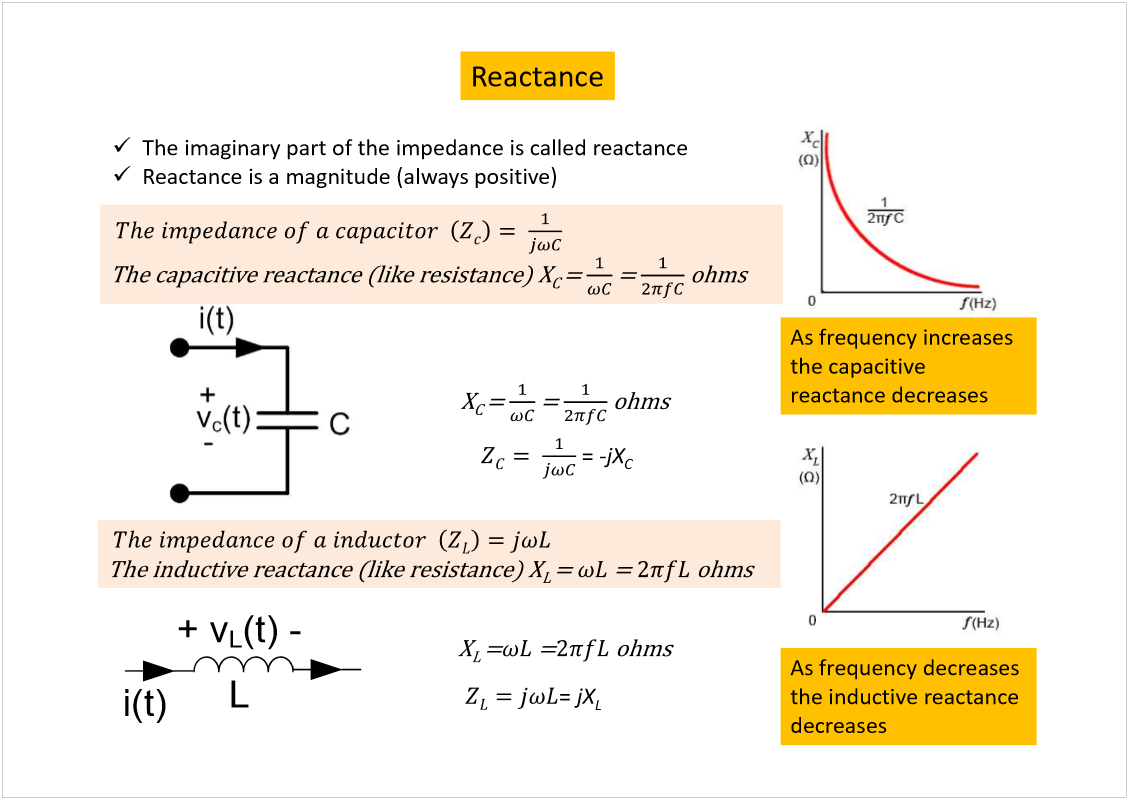
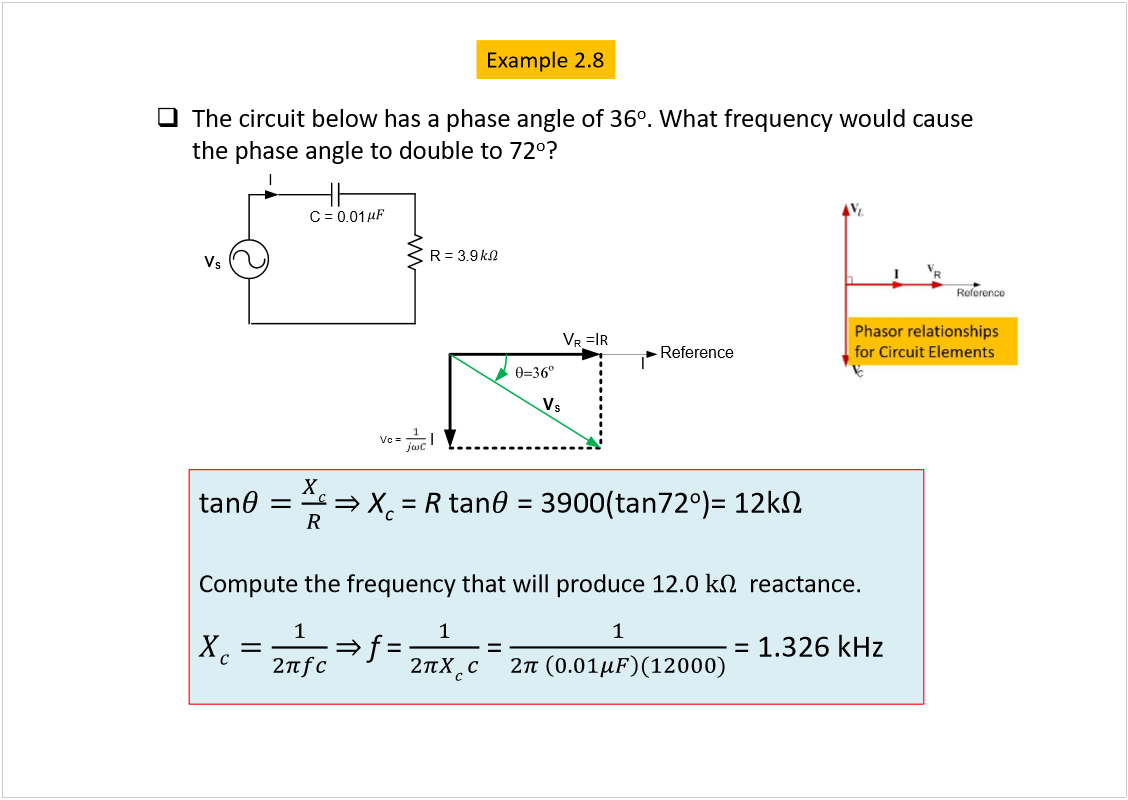
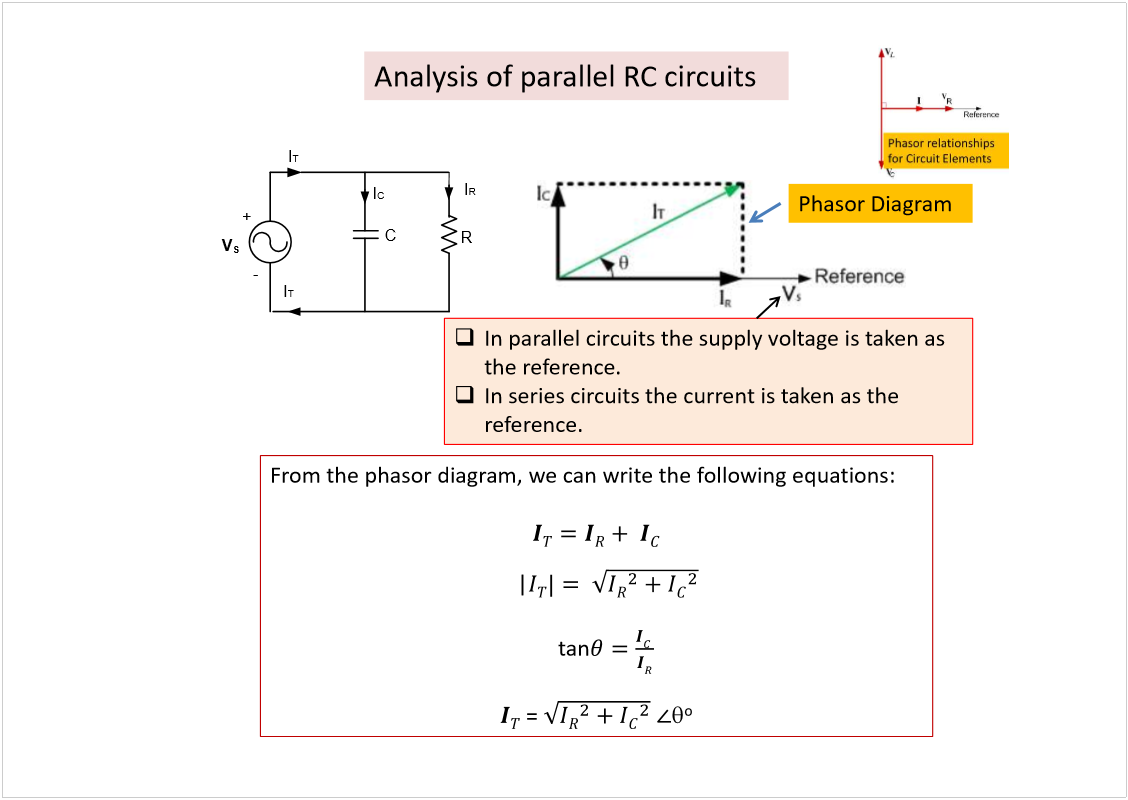
AC Circuit Analysis
Wednesday, 20 February 2019
5:17 PM
<<ELEC2134_Circuits2_ACCircuitAnalysis.pdf>>



![Machine generated alternative text:
Example 2.1
6
Prof E Ambikairajah, UNSW, Australia
Determine the phasorscorresponding to the following sinusoids:
(a)
Therefore
10
o
(b)
v
(
t
) = 7 sin(2
t
+ 40
o
);
v
(
t
) = 7 cos(2
t
-90
o
+ 40
o
) [we know that sin
t
= cos (
t
-90
o
)]
Therefore
0
o
Find the sinusoids represented by the following phasors:
(a)
V
Since
j
0
o
,
0
o
=(
0
o
)(
0
o
)=
o
)
Converting this phasorto the time domain gives
V
(b)
M
= 5 and
= 126.87
o
o
.
Transforming this into time domain gives
i
A
Example 2.2](AC%20Circuit%20Analysis_files/image006.png)
![Machine generated alternative text:
Example 2.3
Two sine wave sources are shown in series across a load.
Find the total voltage
V
S
=
V
A
+
V
B
=
+
= 60
+ 30
=[60 cos60
o
+
j
60 sin60
o
] + [30 cos30
o
+
j
30 sin30
o
]
= 56 +
j
67
7
Prof E Ambikairajah, UNSW, Australia
R
L
ohms
V
B
=30V
30
o
V
A
=60V
60
o
V
S
o
0
o
V
A
=60V
V
B
=60V
Reference
Phasordiagram
cos(
) +
sin(
)
Convert to
polar form
Magnitude =
= 87.3 V
=
= 50.2
o
= 87.3V](AC%20Circuit%20Analysis_files/image007.png)

|
|
|||
|
|
 |
||
|
|
 |
||
|
|
|||
|
|
 |
||
|
|
|||
|
|
 |
||
|
|




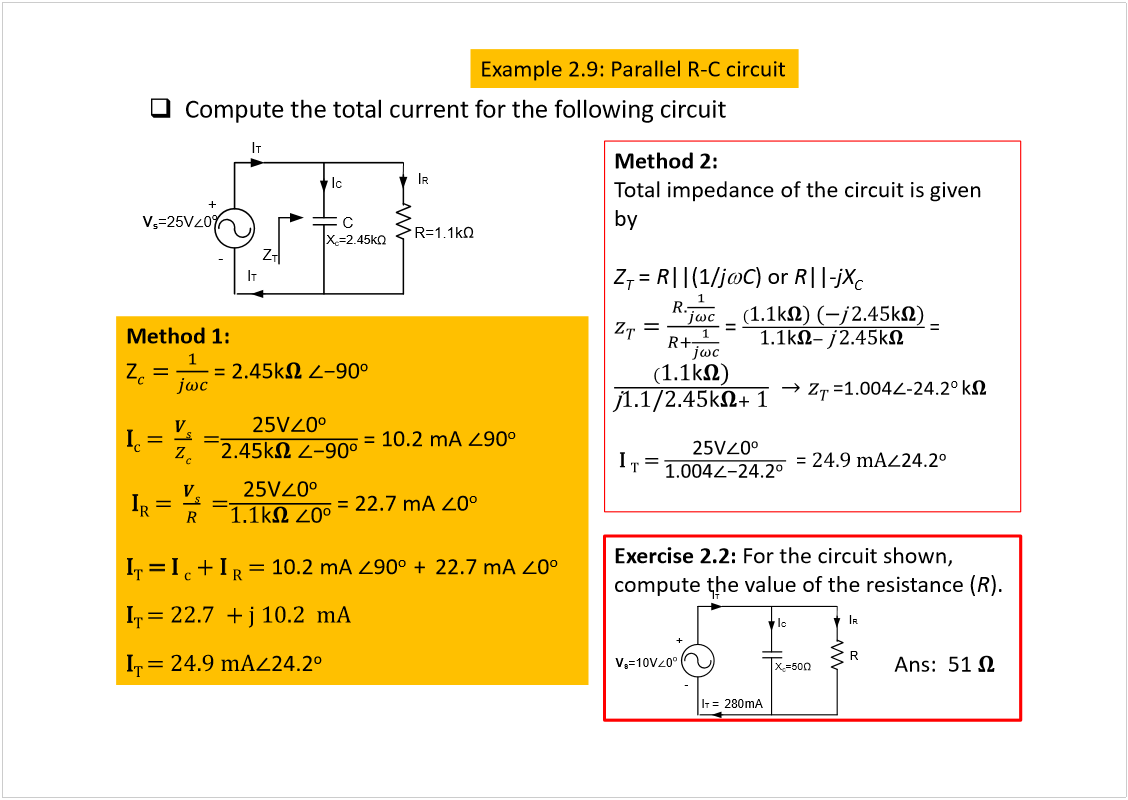
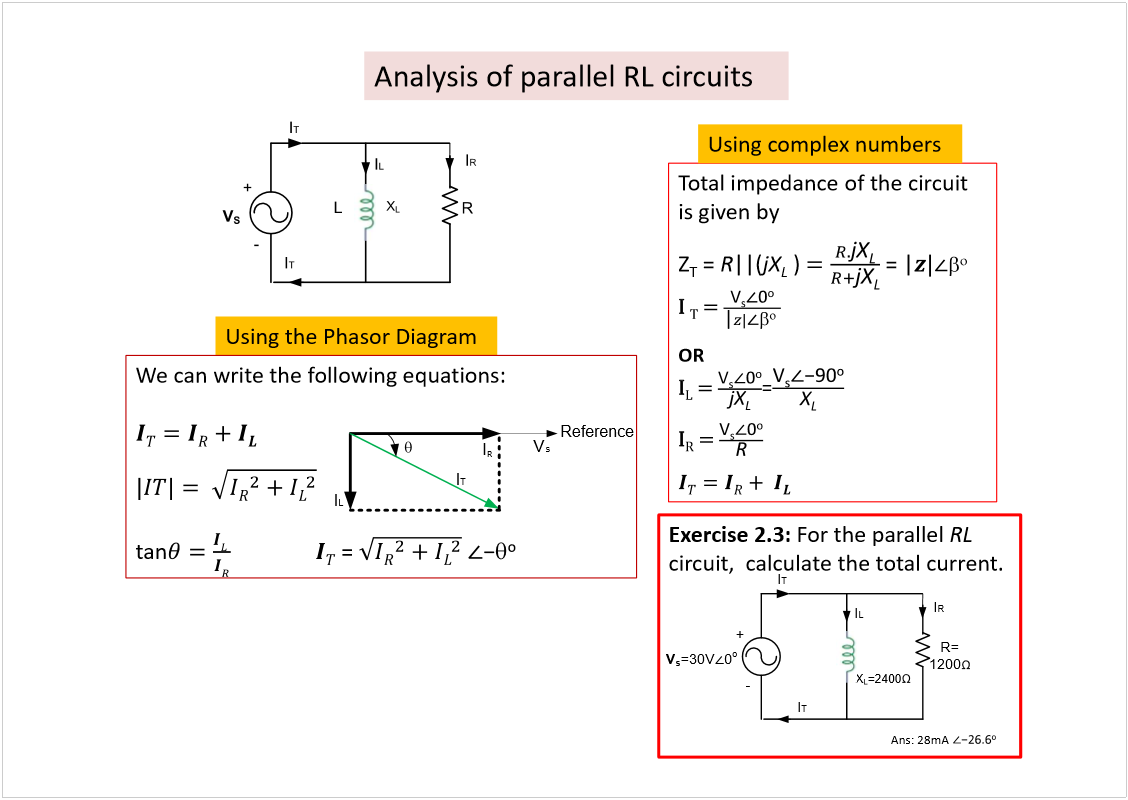
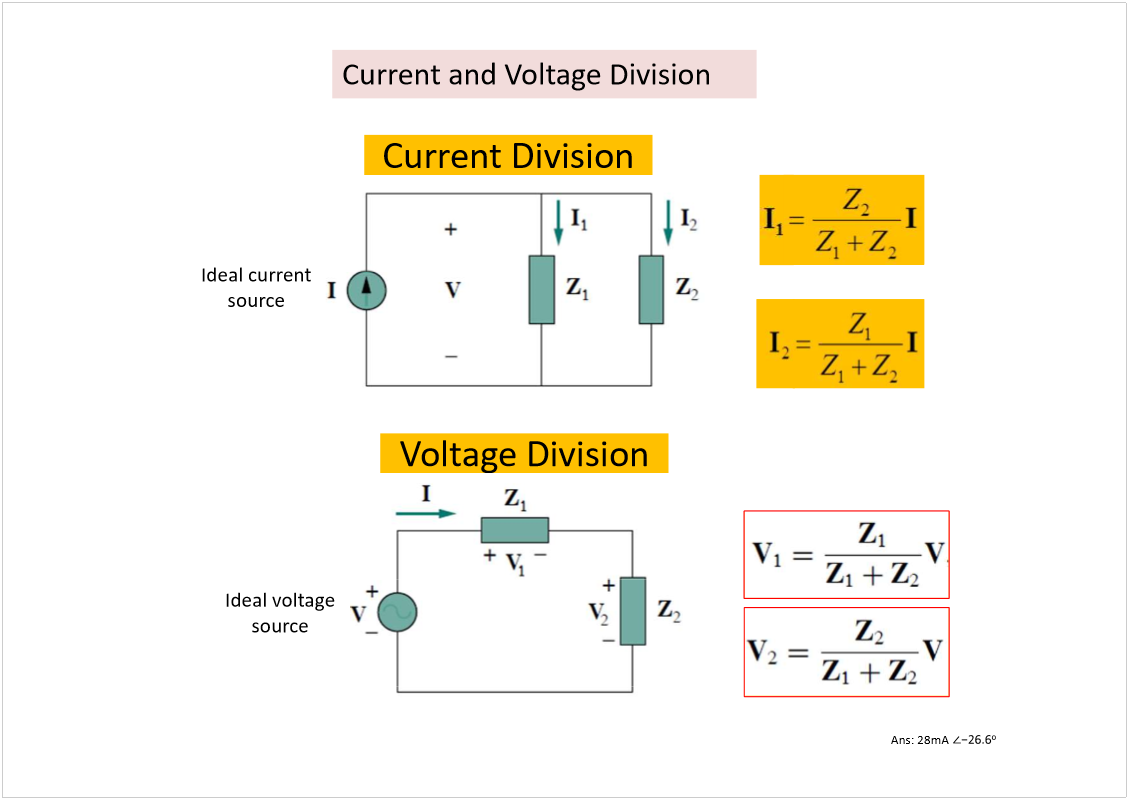

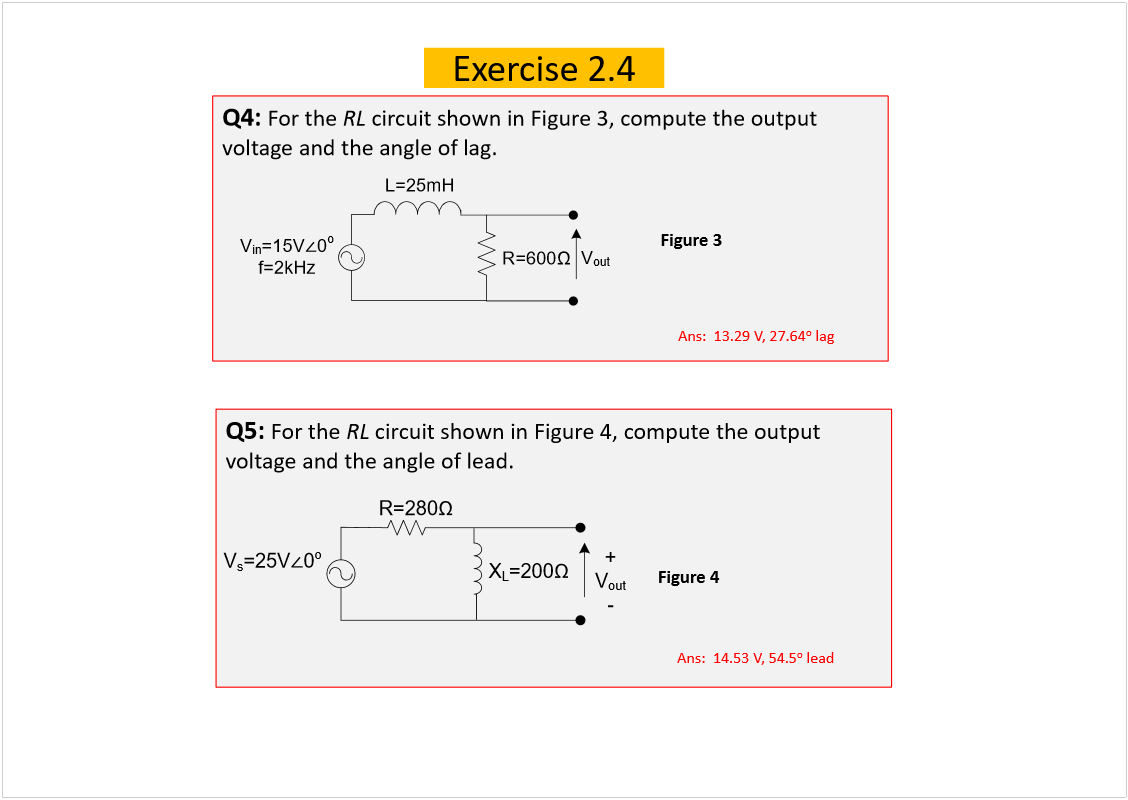
![Machine generated alternative text:
Example 2.11: RLC circuit [4]
Find the steady-state current for the circuit shown below. Find the phasorvoltage
across each element and construct a phasordiagram.
I
+
-
I
V
i
=100V
30
o
=500rad/sec
+
+
+
-
-
-
R=100
V
R
V
L
V
C
L=0.3H
C=40
F
Ê
ã
Z
L
=
j
L
=
j
(500) (0.3) =
j
150
Z
C
= (1/
j
C
) =
= -
j
50
The total impedance:
Z
T
=
R
+
Z
L
+
Z
C
=100+
j
150
ó
j
50 = 100 +
j
100
Z
T
=
The Current
I
×
ã
ã
= 0.707
-15
o
Ê
Î
ã
(0.707
-15
o
) = 70.7
-15
o
Ê
Ô
ã
= (150
90
o
) (0.707
-15
o
)=106.1
75
o
Ê
Ý
ã
= (-
j
/
C
)
= (50
-90
o
) (0.707
-15
o
)
= 35.4
-105
o
I
V
R
Reference
(0
O
)
|V
R
|= 70.7
V
C
|V
C
|= 35.4
V
L
|V
L
|= 106.1
V
S
|V
S
|= 100
-15
o
30
o
75
o
PhasorDiagram](AC%20Circuit%20Analysis_files/image027.png)
![Machine generated alternative text:
Example 2.12: Series and Parallel combinations of complex impedances [4]
Q2:
For the circuit shown below, Find the current through each element and construct
a phasordiagram showing the currents and the source voltage.
Ê
·
ã
and
= 1000 rad/sec
Z
L
=
j
L
=
j
(1000) (0.1) =
j
100
Z
C
= (1/
j
C
) =
= -
j
100
Z
RC
=
=
= 70.71
-45
o
Z
RC
=
Ê
Ý
ã
= 10
-180
o
Now we compute the current in each element
×
ã
ã
= 0.1414
-135
o
×
Î
ã
=
= 0.1
-180
o
×
Ý
ã
=
ã
0.1
-90
o
I
R
Reference
I
C
-135
o
I
V
L
PhasorDiagram
I
+
-
I
R
I
C
v
i
(
÷ ã ïð
øïððð
ó çð
±
÷
C=10
F
+
-
V
C
+
-
R=100
V
R
L=0.1H
+
-
V
L
V
i
V
i
=10V
-90
o
X
L
= j
L
I
+
-
+
-
V
C
+
-
V
L
Z
RC](AC%20Circuit%20Analysis_files/image028.png)


![Machine generated alternative text:
[1] Alexander, C. K., & Sadiku
th
edition, McGraw Hill.
th
edition, Wiley & sons.
School of Electrical engineering and Telecommunications, UNSW,
Australia.
[4] Hambley
Publishing.
References](AC%20Circuit%20Analysis_files/image033.png)
AC Circuit Analysis
Wednesday, 20 February 2019
5:17 PM





![Machine generated alternative text:
Example 2.1
6
Prof E Ambikairajah, UNSW, Australia
Determine the phasorscorresponding to the following sinusoids:
(a)
Therefore
10
o
(b)
v
(
t
) = 7 sin(2
t
+ 40
o
);
v
(
t
) = 7 cos(2
t
-90
o
+ 40
o
) [we know that sin
t
= cos (
t
-90
o
)]
Therefore
0
o
Find the sinusoids represented by the following phasors:
(a)
V
Since
j
0
o
,
0
o
=(
0
o
)(
0
o
)=
o
)
Converting this phasorto the time domain gives
V
(b)
M
= 5 and
= 126.87
o
o
.
Transforming this into time domain gives
i
A
Example 2.2](AC%20Circuit%20Analysis_files/image006.png)
![Machine generated alternative text:
Example 2.3
Two sine wave sources are shown in series across a load.
Find the total voltage
V
S
=
V
A
+
V
B
=
+
= 60
+ 30
=[60 cos60
o
+
j
60 sin60
o
] + [30 cos30
o
+
j
30 sin30
o
]
= 56 +
j
67
7
Prof E Ambikairajah, UNSW, Australia
R
L
ohms
V
B
=30V
30
o
V
A
=60V
60
o
V
S
o
0
o
V
A
=60V
V
B
=60V
Reference
Phasordiagram
cos(
) +
sin(
)
Convert to
polar form
Magnitude =
= 87.3 V
=
= 50.2
o
= 87.3V](AC%20Circuit%20Analysis_files/image007.png)



|
|
|||
|
|
 |
||
|
|
 |
||
|
|
|||
|
|
 |
||
|
|
|||
|
|
 |
||
|
|












![Machine generated alternative text:
Example 2.11: RLC circuit [4]
Find the steady-state current for the circuit shown below. Find the phasorvoltage
across each element and construct a phasordiagram.
I
+
-
I
V
i
=100V
30
o
=500rad/sec
+
+
+
-
-
-
R=100
V
R
V
L
V
C
L=0.3H
C=40
F
Ê
ã
Z
L
=
j
L
=
j
(500) (0.3) =
j
150
Z
C
= (1/
j
C
) =
= -
j
50
The total impedance:
Z
T
=
R
+
Z
L
+
Z
C
=100+
j
150
ó
j
50 = 100 +
j
100
Z
T
=
The Current
I
×
ã
ã
= 0.707
-15
o
Ê
Î
ã
(0.707
-15
o
) = 70.7
-15
o
Ê
Ô
ã
= (150
90
o
) (0.707
-15
o
)=106.1
75
o
Ê
Ý
ã
= (-
j
/
C
)
= (50
-90
o
) (0.707
-15
o
)
= 35.4
-105
o
I
V
R
Reference
(0
O
)
|V
R
|= 70.7
V
C
|V
C
|= 35.4
V
L
|V
L
|= 106.1
V
S
|V
S
|= 100
-15
o
30
o
75
o
PhasorDiagram](AC%20Circuit%20Analysis_files/image027.png)
![Machine generated alternative text:
Example 2.12: Series and Parallel combinations of complex impedances [4]
Q2:
For the circuit shown below, Find the current through each element and construct
a phasordiagram showing the currents and the source voltage.
Ê
·
ã
and
= 1000 rad/sec
Z
L
=
j
L
=
j
(1000) (0.1) =
j
100
Z
C
= (1/
j
C
) =
= -
j
100
Z
RC
=
=
= 70.71
-45
o
Z
RC
=
Ê
Ý
ã
= 10
-180
o
Now we compute the current in each element
×
ã
ã
= 0.1414
-135
o
×
Î
ã
=
= 0.1
-180
o
×
Ý
ã
=
ã
0.1
-90
o
I
R
Reference
I
C
-135
o
I
V
L
PhasorDiagram
I
+
-
I
R
I
C
v
i
(
÷ ã ïð
øïððð
ó çð
±
÷
C=10
F
+
-
V
C
+
-
R=100
V
R
L=0.1H
+
-
V
L
V
i
V
i
=10V
-90
o
X
L
= j
L
I
+
-
+
-
V
C
+
-
V
L
Z
RC](AC%20Circuit%20Analysis_files/image028.png)




![Machine generated alternative text:
[1] Alexander, C. K., & Sadiku
th
edition, McGraw Hill.
th
edition, Wiley & sons.
School of Electrical engineering and Telecommunications, UNSW,
Australia.
[4] Hambley
Publishing.
References](AC%20Circuit%20Analysis_files/image033.png)
Created with Microsoft OneNote 2016.