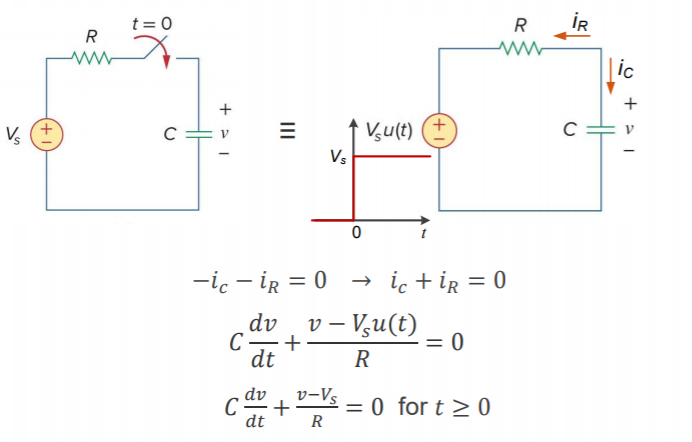
Step Response of RC Circuit

Monday, 27 August 2018

12:31 PM

The step response is the response of the circuit due to a sudden change in DC voltage or current.

  • It is the circuit behaviour when the input/excitation is the step function
  • We can model this behaviour with a switch opened or closed at

 

A unit step function, denoted by  is:

 for negative values of time

 or positive values of time

 

It serves as a good approximation to switching signals representing a sudden change in voltage or current

 

To analyse the step response, we can use KCL at the node between the resistor and capacitor

Machine generated alternative text: ic dt dv dt Vsu(t) v - vsu(t) v-vs = 0 for t 2 0

 

Machine generated alternative text: Solve differential equation: dv v—V Rearrange: S = O, t 20 dt dv -1 (V ¯ Vs) —1 Separate: Integrate: Solve for v(t): Apply initial conditions V(0) = vs = vo 1 dv = dv = dt RC v(t) —t In(v — Vs) ¯ v(t) — Vs = eRC —t = Vs + (vo — Vs)eFC , t 0

 

Machine generated alternative text: • No need to derive the differential equation solution every time, just use the result. • The result shows that the voltage response of the RC circuit will change from the initial Vo to the value of Vs in an exponential manner. Depending on the value of initial conditions Vo and voltage source Vs, the capacitor can be charged or discharged. o, v(t) = Vs + (Vo — Vs)e RC, v(t) Vsu(t) v(t)

 

Machine generated alternative text: • The concept of time constant also applies to step response. The time constant of a circuit is the time required for the response to decay to l/e (or 36.8%) of its initial value or to increase to 1 — l/e (or 63.2%) of its final value. It is denoted by T. • After 5 time constants (5r), the capacitors is again considered as open circuit as its voltage is no longer changing. 0.632Vs — Vs > Vo v(t) = o, Vs + (Vo — Vs)e-F,

 

Machine generated alternative text: • The step response has two components: v(t) = vs + — vs)eT, t > o v(t) = Voe-F + Vs(l — e¯7), t > O Natural response Forced response Due to stored Due to Independent energy sources Complete response = natural response + forced response v(t) = vn(t) + vr(t), t > O This can be viewed as superposition principle in RC circuits for two sources of energy powering the circuit: 1. Initial conditions (stored energy) 2. Independent sources

 

Machine generated alternative text: • From another perspective: The transient response is the circuit's temporary response that will die out with time. The steady-state response is the behaviour of the circuit a long time after an external input/excitation is applied (after 5 time constants, 5T). v(t) = vs + - vs)e-i, t > O Steady-state Transient response response Permanent Temporary part part Complete response = transient response + steady-state response v(t) = vt(t) + vss(t), t > O

 

Machine generated alternative text: Step response of RC circuit • More specifically: 1. First stage of steady-state There has been no change in the circuit for a long time and the capacitor is an open circuit with v(O) = Vo. 2. Transient stage (O < t < 5T): The capacitor's voltage changes exponentially. 3. Second stage of steady- v(t) First stage of Transient stage state (t > 5T): steady-state Second stage of steady-state The capacitor's voltage reaches its final value or steady-state value and becomes open circuit again with v(t) = Vs when t co or v(Ø) = Vs v(t) = vs + (Vo — vs)eT, v(t) = v(oo) + [v(O) — t > O

 

Machine generated alternative text: Step response of (complex) RC circuit • The step response solution has been derived for a circuit with one single capacitor and resistor. • It is possible to find the voltage across a capacitor in a complicated circuit with multiple resistors, switches, independent and dependent sources by replacing the circuit with its Thevenin equivalent circuit. Resistive circuit with a switch — or -2>5 RTh b VTh c

 

Machine generated alternative text: Step response of RC circuit • Follow these steps to find step response of RC circuits: 1. Find the initial voltage v(O) at t = O across the capacitor before any changes in the circuit (t < O). The capacitor is assumed to be an open circuit. 2. Find the final voltage v(co) or VTh a, at t -+ 00 across the capacitor after the changes in the circuit (t 2 0). 3. Find the time constant T = RTh coc after the changes in the circuit RTh_00 is Thevenin equivalent resistance after the changes (t 0). 4. Calculate the voltage across the capacitor as: v(t) = v(co) + [v(O) — Find any other circuit variable using the capacitor's voltage. 5. Note: A switch which opens or closes can remove part of the circuit or add something to it.

 

Machine generated alternative text: Time shift in step response of RC circuit • Note that if the switch changes position at time t = to instead oft = O, there is a time delay in the response which can be expressed as time shift in the equation. This method can be used for multiple switching at different times. —(t—to) v(t) = v(oo) + [v(to) — T

 

 

Created with Microsoft OneNote 2016.