• FFT exploits the symmetry to convert a calculation that original takes O(n^2) multiply, into an O(n log n) operation
• Divide and conquer on the symmetry of the matrix

Understanding the Recursive Structure

2-point DFT

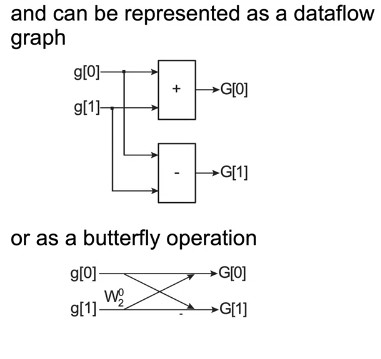
Note the (-) sign next to G[1]. Evaluates to g[0] (-) g[1]

4-point DFT

--> A 4 point DFT can be represented as two sets of 2-point FFTs and a third one

n-point DFT structure

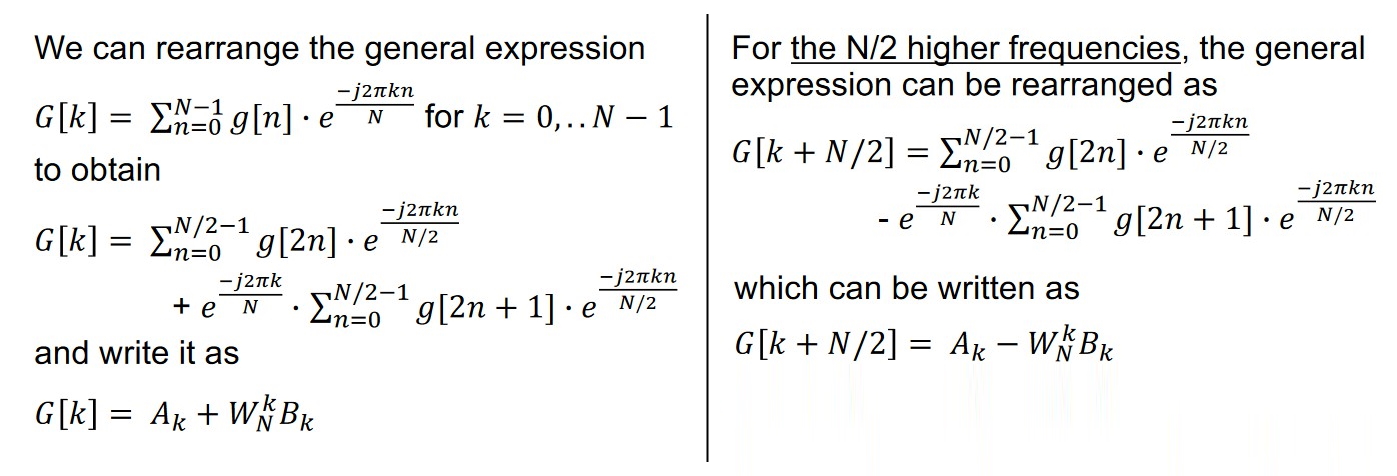
Sum of the even samples, plus the sum of the odd samples scaled by a value
aka function of the even terms plus the scaled sum of the odd terms

In the above, we split the algorithm into two functions so that we can perform operations in parallel

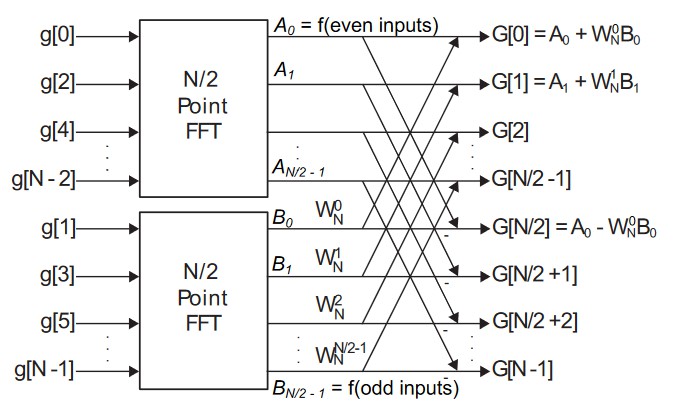
8-point FFT

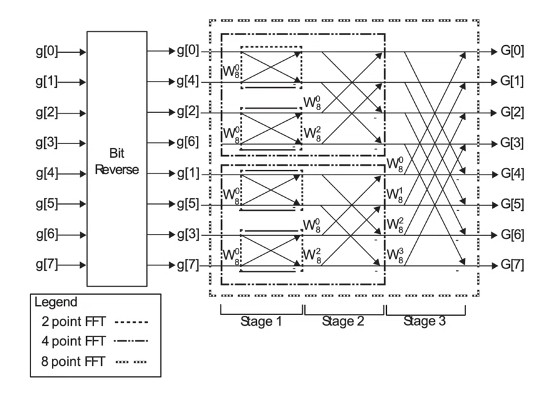
• Perform separate 4-point FFTs on the even and odd values
  • And as such, each 4-point FFT has two 2-point FFTs

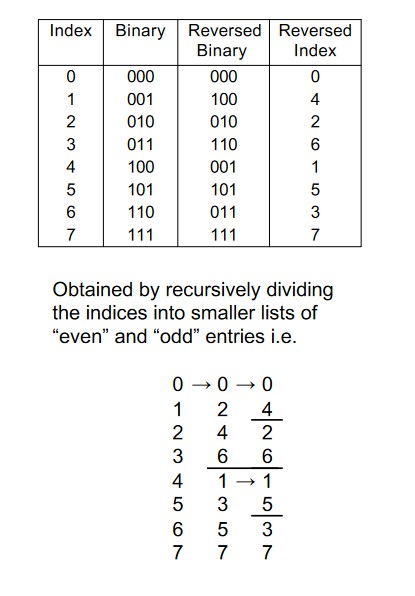
On Bit-Reversal

How many calculations?

Each butterfly operation takes 3 calculations (multiply, addition, subtract).
So in n log n operations, there are 3n log n calculation.

Note that there are more steps to each multiplication (i.e. calculation of real and imaginary values)

...

How many stages does a 64-point FFT have?

Two 32-point, each having two 16-point, each having two 8-point, etc...
There are 6 stages (i.e. 2^6)

What index does g[37] have in a 64-point FFT?

dec(37) = bin(100101)

0b101001 = 41

How many butterfly operations are there per stage in a 64-point FFT

There are N/2 operations on each stage -> so there are 32 butterfly operations in a 64-point FFT

Cooley-Tukey FFT

Since each butterfly operation is independent of the other operations in the same stage, we can (theoretically) perform all operations (there are n/2 of them) per stage.
The task interval can then be 1 (note whilst it may take several clock cycles to complete e.g. the computations), the time between stages is really just 1

Theoretically a 1024-point FFT running at 250MHz could then operate at 1024 points * 4 bytes per point * 2 values [real, imaginary] * (250 * 10^6) = 2 TB/s ... We probably don't have the power requirements, nor resources to achieve it. Also 🔥🤒

That FFT operation, if having a task interval of 1, would be processing 1024/2 * 250 * 10^6 = 128 gigops/s

Only feasible to parallelise a small set of samples

Software Implementation

Firstly, we perform a bit-reversal on the inputs to set them up in the right order

Then after, stage loop (log_2 size times)
* Butterfly loop
* Inside each loop, compute all butterflies which use the same twiddle factor

Reverse Bits

1
2
3
4
5
6
7
8
9

// reverse the bits of input integer
unsigned int reverse_bits(unsigned int input) {
  int i, rev = 0;
  for (i = 0; i < M; i++) {
    rev = (rev << 1) | (input & 1);
    input = input >> 1;
  }
  return rev;
}

Note: When unrolling, synthesis can detect that these wires are just being remapped, and just rewire it

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21

void bit_reverse(DTYPE X_R[SIZE], DTYPE X_I[SIZE]) {
  unsigned int reversed;
  unsigned int i;

  DTYPE temp;
  for (i = 0; i < SIZE; i++) {
    reversed = reverse_bits(i); // Find the bit-reversed index

    if (i <= reversed) {
      // Swap the real values
      temp = X_R[i];
      X_R[i] = X_R[reversed];
      X_R[reversed] = temp;
      
      // Swap the imaginary values
      temp = X_I[i];
      X_I[i] = X_I[reversed];
      X_I[reversed] = temp;
    }
  }
}

• if (i <= reversed) {...
  • Only need to reverse once; so effectively, just do SIZE/2 switches?
• Could pipeline the real and imaginary arrays

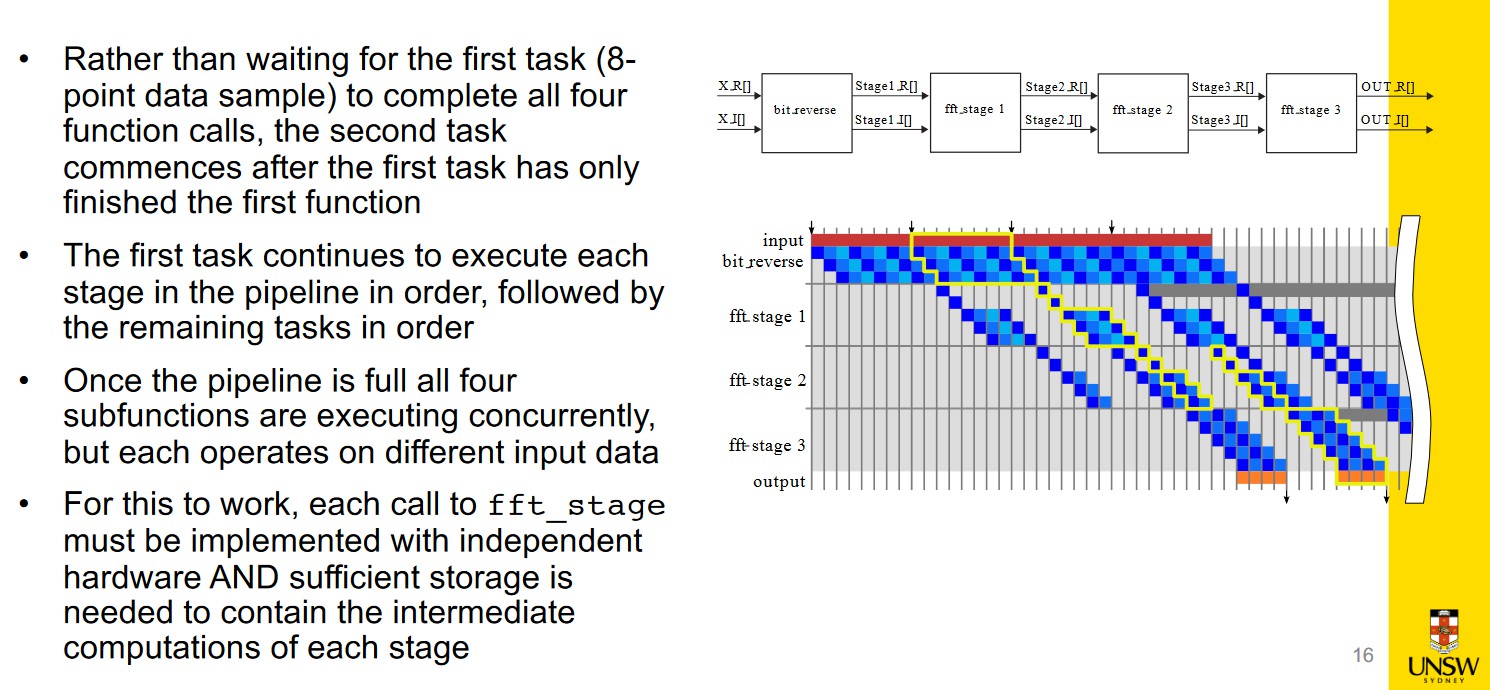
Task Pipelining

HLS will attempt to execute functions in parallel, creating memory and control structures

After the first sample has been bit-reversed and goes into the first FFT stage, the next set of samples can start

See more here