Introduction to Synthesis
Contents
| Name | Expression | Gate |
|---|---|---|
| Logical AND | $ x_1 \cdot x_2 $ | 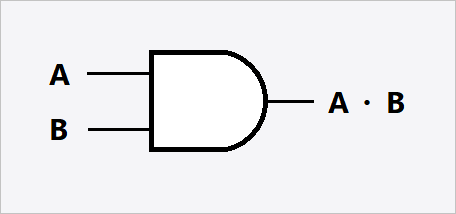 |
| Logical OR | $ x_1 + x_2 $ | 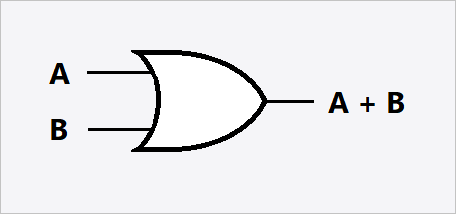 |
| NOT | $ \overline{x} $ | 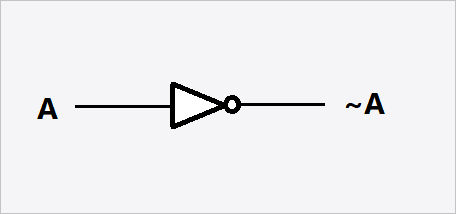 |
Truth Table
A truth table is a mathematical table used in logic-specifically in connection with Boolean algebra, boolean functions, and propositional calculus-which sets out the functional values of logical expressions on each of their functional arguments, that is, for each combination of values taken by their logical variables.
Describes the outputs for all combinations of given inputs.

Operation Logic Order
NOT -> AND -> OR
Boolean Algebra


Circuit Cost
- number of transistors used ~= circuit area
- circuits with fewer gates, and gates with fewer inputs require fewer transistors
Simplified Cost:
# gates + # gate inputs
Example
| Network | # Gates | # Inputs | Cost |
|---|---|---|---|
 | 6 | 11 | 17 |
 | 2 | 3 | 4 |
Synthesis
Hardware synthesis is the process of generating a hardware schematic from a set of inputs
Add a product (AND) term for each row in the truth table with function value $f = 1$
Form the sum (OR) of these terms to produce the function $f$
Simplify the expression using Boolean algebraic manipulation
Draw the circuit, complementing inputs where necessary, using AND gates for the product terms and OR-ing these together
Minterms
A minterm is a product term (AND) where each component of the term appears only once (regardless of complement)

Note that $m_i = 1$ in row $i$ of the truth table and $m_i = 0$ in all other rows
Sum of Products Form
A logic expression consisting of product (AND) terms that are summed (OR-ed) is said to be in the sum-of-products (SOP) form.
A function f can be represented by an expression that is written as a sum of minterms, where each minterm is AND-ed with the value of $f$ for the corresponding valuation of input variables
If each product term is a minterm, then the expression is called a canonical sum-of-products for the function $f$. Every Boolean function has just ONE canonical SOP representation

Maxterms
Maxterms take the complement of minterms
| Minterm equivalent | Maxterm equivalent |
|---|---|
 |  |
Product of Sums Form
If a given function $ f $ is specified by a truth table, then its complement $ \overline{f} $ can be represented by a product of maxterms for which $ \overline{f} = 1$, which are the rows of $f$ where $f = 0$
$ f = \overline{m_2} = M_2 = \Pi{(M_2)} = \Pi{M(2)} $
A logic expression consisting of sum (OR) terms that are factors of a logical product (AND) is said to be of the product-of-sums (POS) form
If each sum term is a maxterm, then the expression is called a canonical product-of-sums for the given function
Exercise

$ f = \sum{m(1,4,5,6)} = TIM(0,2,3,7) $

Summary
